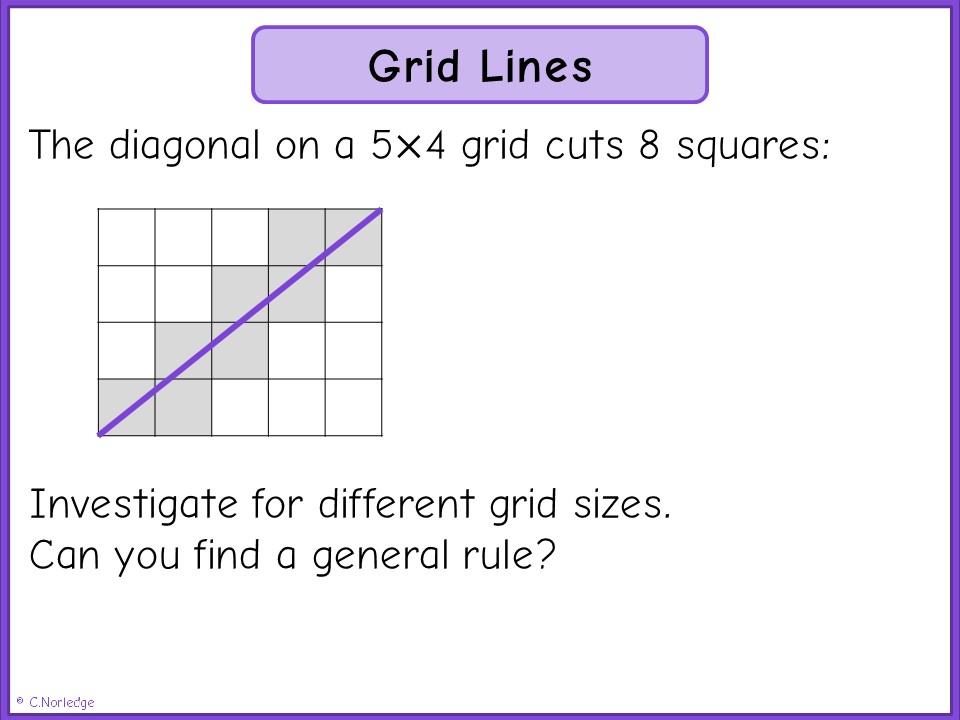
For my remaining full week, I’m going to try and post one rich resource and discussion. I found a nice prompt yesterday in a pack of really old investigations, and thought I’d look into it in a little more detail today. I’d got this filed under HCF and LCM, and have no idea of the origin, but it looked pretty simple so I sat down with pen and paper to try and figure it out.
It turns out it’s not quite as simple as I thought; there’s definitely plenty of scope for practice using factors, multiples and systematic working with this one.
Essentially, it comes down to:
Number of cuts = (Length + Width) – HCF
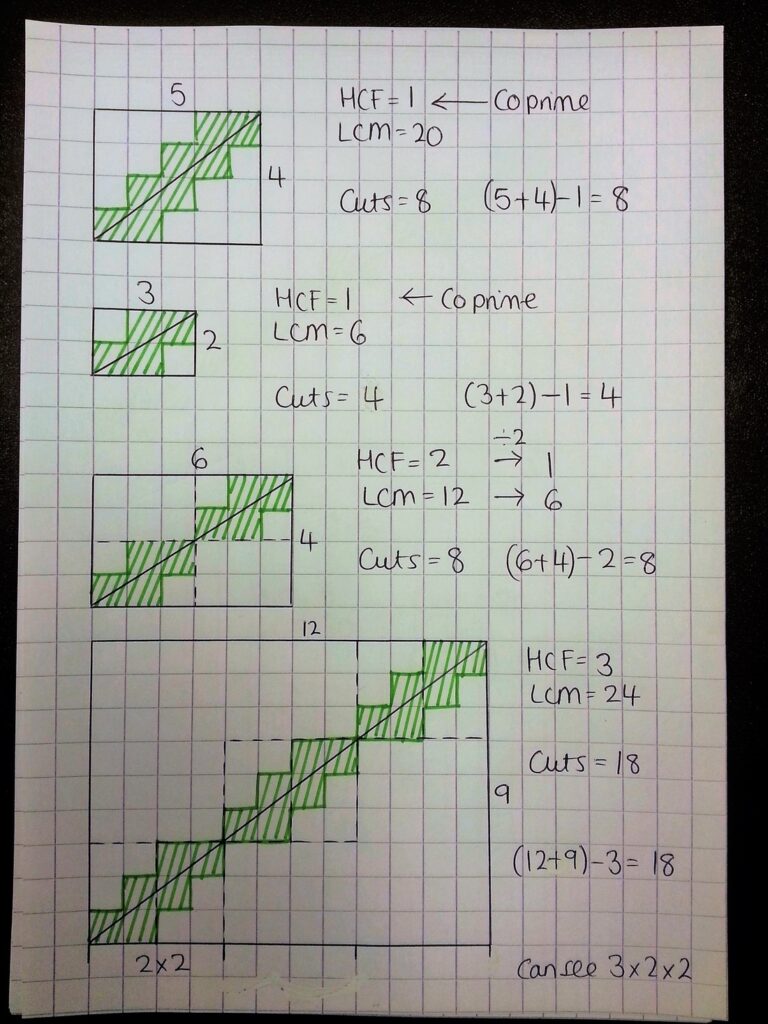
In cases where the length and width are co-prime (have a highest common factor of 1), it’s quite easy to spot.
It’s interesting to explore the links between the 3×2 grid and the 6×4 grid. Multiplying the length and width by 2 has the effect of multiplying both the HCF and the LCM by 2. If pupils connect that grid size = HCF x LCM, there’s an interesting discussion to be had here around length and area scale factors.
I also really like the connection to prime factors. It’s easiest to see on a bigger grid – we can split the cut on a 12×9 into 3 lots of a 4×3 cut, creating a building block for other sizes – so you could ask pupils how many crossings in a 16×12, or 20×15, or just get them to find other grid sizes that fit with this “family”.
If you examine the 4×3 block further, you can see that it’s made of two 2×3 blocks, one a 180 degree rotation of the other. We can view the 2×3 as a base building block – we put two together to give the 4×3 block, then fit 3 of these along the length of the rectangle to complete a side length of 12 (see the diagram, it’s much easier on there!). This gives a lovely visualisation of the product of primes for the side length of each shape.