I attended MathsConf30 in Manchester this weekend, organised by Complete Maths/La Salle Education. MathsConfs are a fantastic day out and always really reinvigorating, and this one didn’t disappoint.
I’m usually hopeless at finishing my MathsConf blogs, so this represents a milestone for me – I think it’s the first one I’ve actually completed since MathsConf5! It’s also ended up loooong – so if you don’t fancy wading through the whole thing, here are some quick links:
- Registration
- Assembly
- Period 1 – Python Workshop for Teachers
- Period 2 – Where to look for world-class resources
- Period 3 – How I wished I’d planned Maths
- Period 4 – Curriculum development futile without effective student revision
- Period 5 – Daydream Interweaver – Reciprocals
Registration
Before leaving my hotel on Saturday morning, I tweeted this:
So I decided the first thing to do was to get cracking with my list! I popped to tuck shop, where Rob (@RJS2212) sold me a pile of delicious goodies, a raffle ticket, and also roped me and a friend into helping out with a balloon popping activity during assembly!
I snaffled a couple of pens from the stands and bought a book, spoiling my list at this point by purchasing from the MA rather than the ATM, but I was dragged in by the front cover of Questions Pupils Ask by Colin Foster, so I’ve added that to my maths shelf!
Assembly
Mark McCourt (@EMathsUK) kicked the day off as usual by welcoming us to MathsConf, and reminding the audience that the last Manchester conference was the day before the first Covid lockdown. It’s fantastic that we’re now back to face to face conferences – you can’t beat the buzz from a day of chatting maths and pedagogy with fellow professionals.
Mark went through the usual whistle-stop tour of Complete Maths, and reminded me that I really need to check it out more often. Mark highlighted the artificial divide between primary and secondary maths, and reminded us that they’re all just children learning maths, so it’s important we understand the entire journey.
It was also very refreshing to be reminded that there are “no party lines” at MathsConf – that we’d all hear things we agreed with and things that challenged us, and having the intellectual debate about these ideas was important.
Andrew Taylor (@AQAMaths) had a quick chat to us about the workshops AQA had to offer (unfortunately I didn’t make either of them) and also signposted the incredibly useful AQA GCSE Maths: Foundation and Higher tier paper improvements booklet in our conference packs; unfortunately I can’t find it published online at the moment, but will update if I do!
Period 1: Python Workshop for School Teachers and Students (Stephen Lynch @DrStephenLynch)
My motivation for attending a coding workshop came from my personal life rather than teaching – more specifically that my husband is currently learning Python for work, and that my dad bangs on about it all the time as the most useful programming language, so I thought I’d see what all the fuss was about.
Stephen’s workshop was billed as entry level; I have very limited knowledge of coding or programming languages (I can manage Hello World in C++ and that’s it), and I found it nicely accessible.
Introduction to Github, Google Colab and some basic code
Stephen introduced us to Github and Google Colab – my descriptions are probably going to be completely off for anyone who actually understands anything about programming, but Github is a place for programmers to share their code, and Google Colab is a space to code without needing to download any additional software. (I fully expect to come back to refine or just full-out rewrite this paragraph when I’ve talked to people with more than 0% programming knowledge!)
Stephen took us through a series of programs, building up from really simple stuff like a straightforward calculation. He highlighted some agreed Python conventions, such as leaving gaps between operators for aesthetic purposes.
We looked at calling functions from one of the Python math libraries, ‘numerical Python’ – Stephen compared these to functions on a calculator. We looked at the floor and ceiling functions, and Stephen highlighted that there are opportunities within coding for students to develop their understanding – for example, when considering the ceiling of -2.5, some students would say -3 rather than -2.
Writing a short program to test integers
We then had a look at some more code, including defining functions (such as squaring), and using if, elif (else if) and else to create a program to test whether integers were positive or negative.

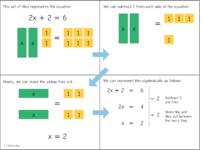
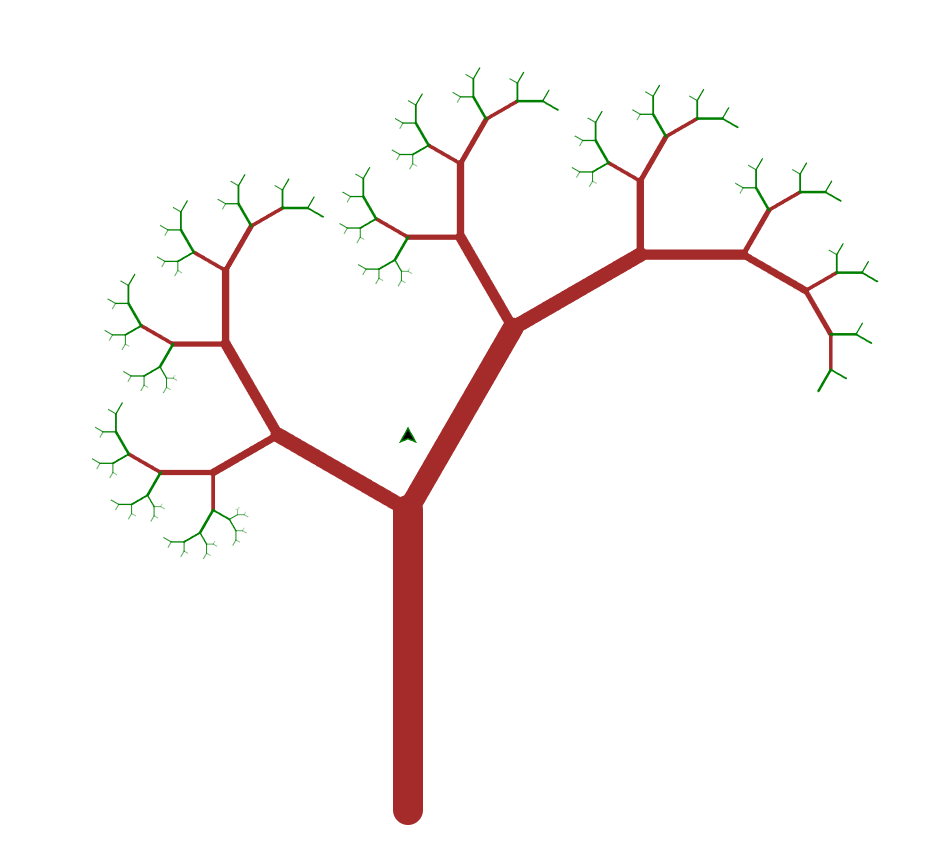
Next we had a look at using something like the Logo turtle within Python to draw a fractal tree. Stephen took us through the program and then explained how he’d use thes with students, challenging them first to change the colours, and then try and work out how to move from a bifurcating tree to a trifurcating tree (which I’m going to have a go at myself!)
The importance of coding for our students
Stephen mentioned the Bond report, which introduced a programming language for all Maths undergraduates, and is being rolled out for other STEM undergraduates shortly. Stephen also mentioned that kids pick coding up really quickly – so we’re going to see students coming through who have seen and are using this stuff from younger ages, and made me reflect on how easy it is to be “left behind” technologically.
While this didn’t seem to have direct applicability as a classroom teacher (a couple of people pointed out that they don’t have time to teach A Level kids the Maths course, let alone add time in for coding in Python), it was an interesting look at entry-level programming, and, if I have time, I’m going to check out a couple of free Python courses myself!
Stephen has kindly shared the conference materials on GitHub if you want to check them out.
Period 2: Where to look for world-class resources (Douglas Butler @douglasbutler1)
I had originally chosen Johnny’s workshop for Period 2, as he was on my “to-see” list – but unfortunately the workshop was so popular that I couldn’t get into the room! So I popped across the hall to see Douglas Butler, and I’m really glad I did.
The title “Where to look for world-class resources” is something that I’d usually go “not for me, I know all of the maths teaching Internet already”. Boy was I wrong?! If you’ve not checked out Douglas’s website (www.tsm-resources.com), it’s absolutely full of the best stuff – some I’d seen before but forgotten about (Gapminder and Vi Hart’s videos were two of these), and some stuff I’d never come across and have bookmarked to check out.
Douglas started off with a quick whistle-stop of Autograph, which I know woefully little about. He highlighted some of his tutorial videos, which will be useful if I ever have the time to upskill myself!
Integer lists on Douglas’s site
The integer lists on Douglas’s site are a curious little quirk, with lists of powers of 2 (linking to discussions about cell doubling, exponential growth and cell death), and Mersenne primes – with Douglas speculating about how Euler in particular knew that M8 was prime in the first place in order to prove that it was so.

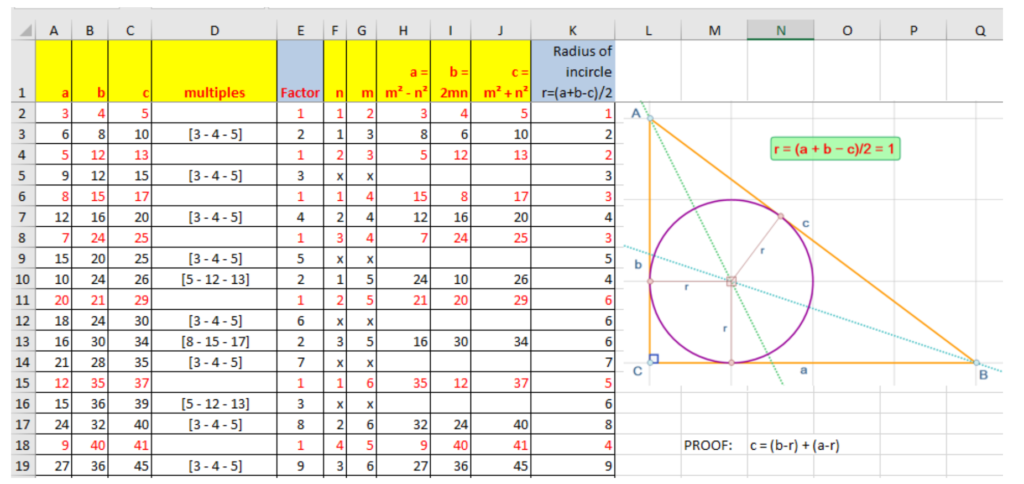
Douglas also took us through the Pythagorean Triples list, including the in-centre radii for each triangle, and I made a mental note to incorporate this into a bit of Pythagorean task design.
Using data sets with Autograph
Next up were the data sets – and there were loads to get our teeth into. I find that I spend a lot of time searching for meaningful data to write statistics-based questions, and Douglas’s site seems like a great one-stop shop! He also demonstrated how easy it was to pull data through from Excel into Autograph and produce visual representations of the data sets – Douglas did a quick demonstration using male life expectancy from the OCR London Boroughs data, which I’ve managed to replicate and add female life expectancy. There’s lots to discuss here!

And finally, a few more new things to check out
A few more new (to me!) websites that I noted down to check out:
- Quibans: News stories or articles that can be used to promote mathematical questions. There’s loads of really rich, proper real world maths here, and definitely merits exploring more!
- Jonny Griffiths: I’ve seen bits of Jonny’s stuff before, but had no idea this site existed, and there’s so much amazing stuff on there.
- Andrew Jeffrey: Douglas mentioned signing up for Andrew’s newsletter, which I have promptly done!
We finished with a look at a superb collection of mathematical images – such as polygons pulled from Google Maps – could students fit a pentagon to an image of the Pentagon?

Period 3: How I wished I’d planned Maths (Dave Taylor @taylorda1
I’ve got to say, I did get somewhat “clickbaited” into this workshop by its clearly original title – so clickbaited that I didn’t realise until I started writing this blog that I went to the wrong workshop, having originally signed up for Key Concepts in GCSE Maths going on next door. No regrets though, as Dave’s session was probably the most I’ve ever laughed in a MathsConf workshop, going for a part-informative, part-stand-up look at how his planning strategies have changed during his teaching career.
Amusing bits aside, it was really curious how much of Dave’s journey reflects mine; I even ended up independently at the same resource-storage strategy (more on this later).
Dave gave us a brief overview of his career, describing how he started out planning lessons for every class he taught, even going as far as planning different lessons for parallel classes. He also described his teaching strategy as teaching how he was taught – a lecture and then a textbook, and for CPD, the only things he attended were the in-house offerings from his school.
The Dunning Kruger curve
Dave showed us the Dunning Kruger curve, which shows the trajectory from novice to expert. Initially, when you don’t know what you don’t know, your confidence levels are high, even though your skill level is really low – you believe you’re great at the thing, even though what you’re doing is probably rubbish (“Mount Stupid”).
There’s then the Valley of Despair, where you suddenly realise how much you don’t know and how bad you are – in the next part of his talk, Dave took us through what he described as the mistakes he made early on in his career, and how changing these things got him out of the Valley of Despair.

Mistake: Teaching how you were taught
Dave circled back to the points from his introduction – how every lesson involved a lecture, followed by a textbook. He pointed out that he was replicating the strategies that had worked well for him, but highlighted that perhaps he (and other mathematicians and maths teachers) had been successful despite these “poor teaching strategies”.
A crucial point for me here was when Dave highlighted being mindful of the effects of the experience we bring to teaching – most maths teachers will have had a very positive experience of learning maths, and many will have done A Level. As Dave put it:
Only 15% do A Level maths – 85% do something different. Your experiences are not the experiences of most kids.
Mistake: Following a scheme of learning to the letter
Rather than blindly following the scheme of learning, Dave discussed how a scheme should be used as a guide, but good planning should also include:
- Looking at prerequisites and making sure that prior knowledge is secure
- Making amendments for what’s on the scheme – there’s no point teaching kids to multiply a 4 digit number by a 2 digit number if they can’t reliably multiply 2 by 2.
- Low floor high ceiling tasks to account for varying start points
Mistake: Finding a resource to match an objective
At this point, Dave did an incredibly entertaining skit about trying to download and save resources from the TES (I definitely saw early career Christine in this bit!) – he suggested that it is often quicker to create the exact resource you need than to search through the whole Internet – and once you’ve made it, share it on Twitter!
While this is a valid point, I wonder whether this is something that gets quicker and easier with experience. Designing a good task or worksheet is much easier when you’ve had experience of what good and bad tasks or worksheets look like, and my task design now usually consists of refining what I already have rather than starting from scratch.
Mistake: Planning lessons for each class
Here Dave suggested that, rather than planning lessons for each class, we should instead be planning lessons for our teaching and planning progressions through topics. So rather than create an individual Notebook/PowerPoint for each lesson, Dave creates a slide deck with all the resources for one topic in the same place – and this deck is the same for any year group.
I started planning like this a while ago, and it’s an absolute gamechanger. A few advantages include:
- You don’t end up with tens of files all called “Adding fractions.ppt” – so then you don’t have to search all of those files to find the one specific task you want
- You’re reminded of excellent tasks that previously worked well, but would otherwise have forgotten about
- It’s much easier to refine your resource collection – rather than saving any and all old rubbish, if something doesn’t work, just delete it out of the slide deck
Dave discussed this later, but I’m slotting it in here as it seems to fit – we should also be planning routines and structures. Dave went through his, which uses the Teach, Do, Practise, Behave model from Complete Maths:
- Teach – Models and metaphors, moving through concrete, pictoral and abstract
- Do – Whole class response, kids replicate, example problem pairs, fluency exercises
- Practise – Mixed practise, retrieval, “red zone” – silence
- Behave – “Problem solving” (whatever that means!), non routine, interesting, be a mathematician
Mistake: Pupils answering questions in class means that the class are learning
Another bingo for early career Christine, along with my reluctance to get out mini-whiteboards because they were “a faff”. Without whole class response systems, only the same few kids answer the teacher’s questions – Dave described these as the “vocal minority”.
He also reflected on his experience as a student – that he would listen carefully while other students were answering questions, most kids aren’t future maths teachers, so probably won’t.
Mistake: Dealing with other people’s expectations of you
This is a big one, and probably isn’t talked about enough. Early on in my career, I was sometimes put off asking for advice on how to teach something because I thought it would look like my subject knowledge wasn’t up to scratch.
Dave highlighted that pedagogic subject knowledge is very different to pure subject knowledge, and the importance of valuing the experience around you.
He also reminded us that it’s OK to say no to things, particularly extra-curricular responsiblities like coaching a football team or running school trips.
Mistake: “I taught it fine, they just didn’t learn it”
Here I jotted down: “You are a teacher, not a broadcaster,” and what a great way to put it. Just covering the content isn’t enough – effective planning needs to ensure that the material students are being taught is actually being learned!
Mistake: “I know maths, I don’t need CPD”
This links back into the previous point about expectations, and I guess here this refers to expectations of yourself. Many maths teachers come in with maths or STEM-related degrees, and while they’re experts in maths, they are novices in knowing how to teach maths.
Dave highlighted a few great sources of CPD, such as books, podcasts and webinars, including a plug for the latest offering from Complete Maths, Teaching Together.
Mistake: Observing behaviour
I’ve definitely been guilty of this, both as a trainee and as a mentor! Dave pointed out that there’s no point going to observe a teacher who has good behaviour management strategies, because you won’t see anything (there won’t be any/much unwanted behaviour!).
Instead, you are much better meeting with these teachers, having a discussion about what they do, and then potentially asking them to observe you teach and discuss further from there,
Mistake: “If we churn out 200 van drivers’ mates, we’ve done a good job”
I can’t remember where Dave had pulled this quote from, but it’s a good illustration of the dangers of low expectations. He reminded us that all pupils can learn well if we find the appropriate content.
Dave also pointed out how important this idea of adaptation in the current situation – for example, the current Year 7s will be significantly different to the “standard” Year 7 intake (if that exists) as they have missed 15% of their usual primary education. A student with a scaled score of 100 this year is very different to a student with the same score from 2019.
Dave finished off by sharing a few more ideas, most of which I’ve already mentioned under the headings above. The final fantastic thing he had for us was his planning spreadsheet for automating retrieval practice, which you can get here:
Period 4: Curriculum development futile without effective student revision (Ed Watson @MrEdWatson)
I did a bit of reading and research on revision strategies for an article for Third Space earlier this year, so this seemed like a nice way to continue that learning journey.
Ed kicked off his session with an overview of the World Memory Championships, where competitors do things like learning decks of cards and digits of pi, discussed in the book Moonwalking with Einstein. Apparently, these memory champions are successful by simply learning and practising techniques to remember things – there’s nothing innate, it’s just about building the right habits and strategies. From this introduction, Ed explained that his workshop was about attempting to do the same for our students.
Improvements to teaching are huge – but how do we get students to memorise what they’ve learned?
Ed highlighted that there’s loads of really good stuff happening with curriculum development, listing principles from cognitive science and more research being used in the classroom. However, this doesn’t mean that all our students will suddenly get grade 9s, even with the best teaching in the world. We need to look at how to instill independence in kids, so they pick up where we leave off.
Ed gave us the example of learning the piano – a music teacher shows and tells you how to do it in your lesson, but if you do no practise before your next lesson, you’re going to make very little improvement. Ed acknowledged that more vulnerable students, or those with a disrupted home life, would likely need more things putting in place to help them.
Students prefer ineffective strategies for revision, because these are easier
Students generally are very bad at knowing how to revise properly. They want to re-read notes and cram, both of which are ineffective strategies. Some know they should be using better strategies, and try these, but then when these are difficult, they revert back to the easy options.
Ed gave us a great example of demonstrating memory strategies to students – getting them to play “Remember my PIN” (don’t use your real one!). Give them the PIN 1536 and see how many of them can remember it in a few minutes – this will probably be most of them.
Then give them a strategy to remember it for longer – for example, how many of them are 15? So the first bit is their age. Then how many have parents who are 36? Those who do can remember their age / parent’s age instead of four random digits. Ed told us that this is one strategy using by memory champions to learn digit strings, along with assigning each digit an image and making up a story.
Long-term memory, working memory and the importance of knowledge
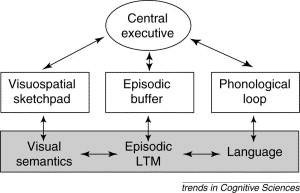
Ed briefly went over the difference between long term memory (practically infinite in capacity) and working memory (holds 7 plus minus 2 items). He described the current model of working memory, which includes the episodic buffer, where experiences from the phonological loop (inner voice) and visuo-spatial sketchpad (inner drawing space).
Historically (thinking back to Ancient Egypt for example), experts were people who could remember things, as there were no books or Internet available, but now it was easier to just Google everything. Ed referenced Daniel Willingham, saying that without knowledge, you can’t understand new information – for example, he’s fluent at reading but wouldn’t understand an article about an unfamiliar specialist subject such as ballet.
The idea of self-testing isn’t new – Ed gave us references from Gates (1917) and James (1890) stating that active repetition better than passive repetition. He even went back as far as Bacon (1620) – reading a book 20 times has less impact than if you read the same book 10 times and test in between. These ideas about testing and memory are hundreds of years old.
Ed suggested viewing knowledge as a spider’s web – the more you know, the easier it is for you to ‘catch’ information and know more.
The memory palace
Next, Ed gave us a 20-item shopping list (strawberries, avocados, tuna, milk, orange juice, and so on) to memorise in two minutes. Once the time was up, we had to write down as many items as we could remember. Due to a mis-spent youth watching far too much rubbish telly, I already had the upper hand here, and employed the idea of a memory palace:
So I imagined opening the door to my house, and seeing some strawberries and avocados sitting on the stairs. Then I go into my kitchen and see that there’s a can of tuna in the cupboard, and someone has left milk and orange juice out on the worktop. I make myself a toothpaste sandwich… and so on. In fact, I can still do the whole list now, in the correct order, three days later – and I’m definitely not a memory champion, I lose my keys on a weekly basis.
Interestingly, the other person who got all 20 has aphantasia, which means that they are unable to visualise imagery – so they just memorised the list by looking at the words and repeating them until each word was memorised. I thought this was a really powerful reminder that we can’t assume strategies will work for all students!
Ed jokingly accused me of being a plant, because he then went on to describe how he’d used a memory palace (his childhood home) to memorise the sequence of his talk in exactly the same way. Similarly to me, he also had weird things going on; as he pointed out, the more inappropriate, weird, rude or horrific an image, the better it will be memorised. This is a strategy that can be employed with students – but with care! Perhaps they don’t need to share their mnemonics for SOHCAHTOA.
In the remainder of the session, Ed shared his steps to successful revision – literally as a graphic of a staircase, which I hope will be available somewhere once the conference materials are shared.
Starting and developing a routine
Getting started is the most difficult step, and students will need support in starting their revision. Students find revision easier once they’re used to the repetition. Getting them to look at the screen time on their social media apps is a great place to start if they say they don’t have the time – Ed gave the example of one student racking up 40 hours a week on Snapchat, which is equivalent to a full-time job!
Ed likened a good revision routine to a roundabout – getting it started is difficult but once you’re off, momentum keeps it going. However, we have to be careful students don’t peak too early, so they probably shouldn’t be doing five past papers a week from September.
Another recommended strategy for creating routine is to make a study schedule, which, according to Cornell and Bjork (2007), only 13% of students do. Once there’s a schedule in place, sharing this schedule makes it more impactful – for example, if students share their schedules with parents, parents can then hold students to account and make sure they’re not just revising their favourite topics.
Flashcards
Ed then discussed how flashcards should be used to support good revision. He suggested that students were better off creating their own materials rather than relying on purchased flashcards, as processing information from class notes and putting this into your own words is more impactful (and consequently, harder work!).
Once students have their flashcards, they proceed as usual – look at the card, look away, try to answer the problem or recall the fact on the card. This is referred to as successive relearning (Dunlosky).
Students may find the Leitner system useful, where learned and unlearned cards are placed in different boxes or piles. Unlearned cards need to be repeated more frequently – perhaps daily – but learned cards only need to be reviewed monthly, for example.
Writing frames
Ed said that writing frames were probably more useful outside of maths, but the idea is that students are provided with frames to structure exam responses mark by mark. Students can then copy the structure to help with unfamiliar problems and contexts.
I jotted down Backwards Faded Exercises at this point – I definitely feel like these are the closest maths comes to a writing frame!
Past papers and video walkthroughs
Ed highlighted past papers as the “golden step” in exam preparation – basically, if you want the top marks, you have to go through loads of past papers. Initially they take ages, as every question seems really difficult, so it’s important that students don’t start too early and are put off.
There are direct and indirect effects of completing past papers. One indirect effect is identifying which topics need to be revised further. But the direct effect is that the process of testing means that students get better.
Ed showed us a few studies looking at practice testing compared to other methods of revision, such as restudy – in all cases, practice testing beat restudy. Unsurprisingly, the impacts are greater on the top third of attainers than the bottom third, but there is still a significant enough improvement that we can say that past papers are key.
Ed pointed out that this doesn’t mean that students should just do past papers – doing a combination of past papers and restudy beats each strategy individually.
Students need to pick up the slack
Ed finalised his workshop by referring again to the great work going on with curriculum development and teaching, but reminded us that ultimately the students need to pick up the slack once the material has been taught – and that we need to explicitly teach them strategies to do so.
Period 5: Daydream Interweaver – Reciprocals (Nathan Day @nathanday314)
I love Nathan’s interweaving resources, so was really excited to hear him talk about interweaving reciprocals in more detail. He did, however, make us do a load of maths in Period 5, which made me feel the pain of every student I’d ever taught who’d complained about having maths last lesson – my brain hurt by the end of this session!
Because a lot of this session was doing and discussing maths, I didn’t make as many notes (and did a lot of scribbling which I don’t think would be particularly interesting to share!), so this section is a little shorter than the others. Nathan has already shared all of the tasks on Twitter, with a PowerPoint to follow, so go and check them out there!
Interweaving and not interleaving!
Nathan kicked us off with a quick definition:
Interweaving is using questions and tasks that bring together multiple different topics from across mathematics.
He pointed out that it was not interleaving, which he cheekily defined as “nobody knows!” (I’m halfway through Paul Rowlandson’s Craig Barton episode on interleaving at the moment, and I’m inclined to agree!).
He also gave us some reasons to interweave:
- Exploring connections between topics that underpin maths;
- Retrieval opportunities (e.g. putting fractions in every topic);
- Going into greater depth with more ideas;
- Including more challenge… and more… you can always include horrible decimals;
- Purpose (sometimes contrived)
Interweaving in and out with reciprocals
Nathan mentioned a couple of topics that we’d immediately think of when we think about reciprocals, namely gradients of perpendicular lines and dividing fractions, and explained that we’d be looking at a load of other ways to include reciprocals in the curriculum.
After having a go at these questions, all of which had 2/5 and 5/2 as their answer, Nathan explained the distinction between interweaving in and interweaving out.
When interweaving in, you bring other topics into reciprocals – many of Nathan’s examples are topics that aren’t usually taught anywhere near reciprocals, but the question sets were really interesting. We looked at:
- Decimals and mixed numbers
- Indices
- Surds
- Standard form
- Bounds
- Equations
All of these questions included an element of “find the reciprocal of…”, either as the command phrase in the question or a very necessary step early on.
When interweaving out, you look for the topic where it occurs naturally. So this would include the two more obvious examples mentioned at the start, but also:
- The harmonic mean (see Nathan’s slides for some great examples with speed, density and inverse proportion)
- Writing a ratio in 1:n and n:1 form
- Enlargements from A to B and back again
- Area and volume enlargements
- Trigonometric ratios
- Proportional relationships
Nathan pointed out that reciprocals crop up wherever there are multiplicative relationships – he suggested we “find these concepts littered around the course and draw attention to them”.
The final set, which I found really intriguing, was Nathan’s example of “Corrections” – although the problems in this set look really different from each other, there’s an underlying theme of some sort of “correction” being applied from a standard case. I’d love to see more examples of this type of interweaving!
Graduation
The conference closed with a few final remarks from the Complete Maths team, sharing some of the tweets and comments from the day, and drawing the raffle. After a day of chatting maths and listening to some fantastic educators, I left very tired but with my head buzzing with new ideas and things to think further about. Roll on MathsConf31!