Thank you, Internet, for wasting my evening. I don’t know how I found this on YouTube – one of my random click-a-thons searching for goodies, and I’m a sucker for “magic maths” tricks. This one is how to square any (two-digit) number mentally.
If you don’t want to watch the video, here’s the basic idea with 33² as an example:
- Work out the difference between 33 and the nearest 10 (in this case, 30). Difference = 3.
- Add the difference to 33 to get 36. Subtract the difference from 33 to get 30.
- Multiply these two numbers together (30 x 36). This is (apparently) the advantage of this method – it’s easier to do 30 x 36 in your head than a four-way decomposition.
- Finally, square the difference (3² = 9) and add it on to 30 x 36 to get a final answer of 1080 + 9 = 1089.
And here’s my workings:
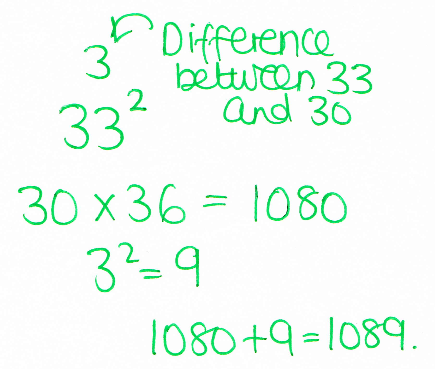
So I did this one…then tried another.
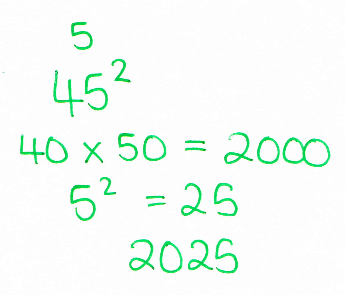
Cute? Convoluted, really, and not particularly workable in the curriculum (I’d much prefer a sensible approach with proper multiplication), but then I got one of those “oh now how does that work?” moments. I could see how it was kinda linked to quadratics and square areas, so I did some doodling. After many aborted attempts, I came up with this:
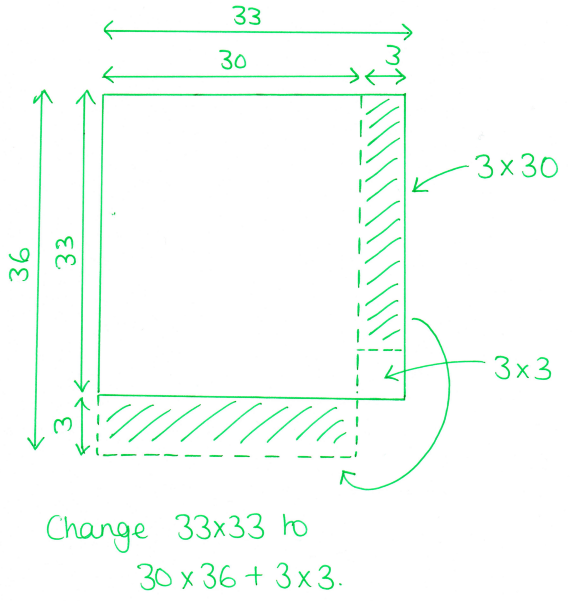
Take a square with side length 33(cm if you insist on units). You can then chop a rectangle off the edge of length 3 (making an easier multiplication of 30 x something) and whack that on the bottom. So then you’ve got a 30 x 36 rectangle, and the little square left over to add on.
Then, because I’m a mathematician and I like doing things properly, I tried to make it work with algebra:
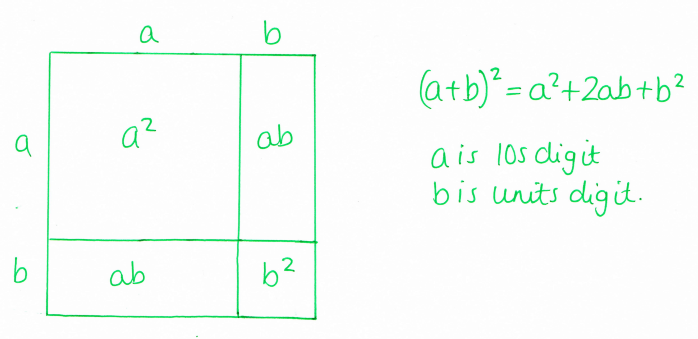
Typical quadratic expansion, but we think about a as the tens digit and b as the units, because we’re trying to change the square into a rectangle with length a (so we have a multiple of 10 to calculate with). Then:
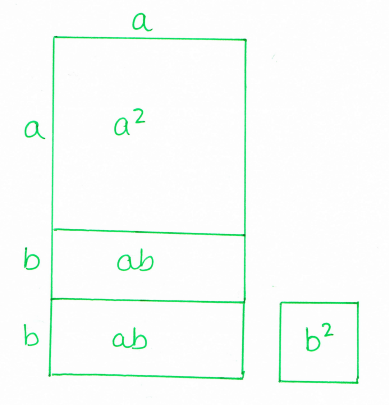
So we’ve changed the problem from (a + b)² (difficult) to a(a + 2b) + b² (messy but easier mentally). I was quite pleased with this!
Just thought this might be a nice challenge problem to give to pupils when working with quadratics (or square numbers for that matter) – show them the video, then get them to explain why it works – numerical or algebraic approach. I do think this lends itself to an exploration of the link between square numbers, area and quadratics, which I think is often overlooked.