Starters can be a contentious issue; the term “starter” is a hangover from the days of three-part lessons in bite-size chunks, which seem to have fallen from vogue now. However, they are still a key part of my teaching, and today’s SBPC looks at why.
In my mind, my lesson “starters” fall into three categories, and they’re not mutually exclusive. Sometimes it’s appropriate to have a couple of “starter” activities (I’m dropping the quote marks now because I’m irritating myself). I once had a lesson starter that went on for the entire lesson, as it became painfully apparent that the class had completely forgotten to solve simultaneous equations, so my quick prior knowledge check turned into an off-the-cuff revision session.
I remember one lesson observation when I was told off for getting pupils to spend five minutes working on problems similar to those they’d solved in the previous lesson. I was told that they weren’t making measurable progress during this five minutes. I was only a newbie at the time, so didn’t want to argue with my observer, so nodded along, decided that I’d make sure I didn’t do it in observed lessons in future, but carried on doing it as part of my standard teaching practice.
I still think that it’s really important to spend some time each lesson getting pupils to practise skills they’ve already learned. Read about the Ebbinghaus Forgetting Curve and this all starts to make sense (while you’re at it, read this post about blindly accepting research too – it’s good to know that Ebbinghaus is fine).
Pupils often ask me why I’m “so good at maths”. My response is that I use it every day – there’s not something innate in me that makes me a mathematician. I tell them about how I had to re-learn my times tables when I started teaching – although I’d learned them before, I was very rusty and my recall wasn’t as snappy as I would have liked, due to over-reliance on a calculator at university.
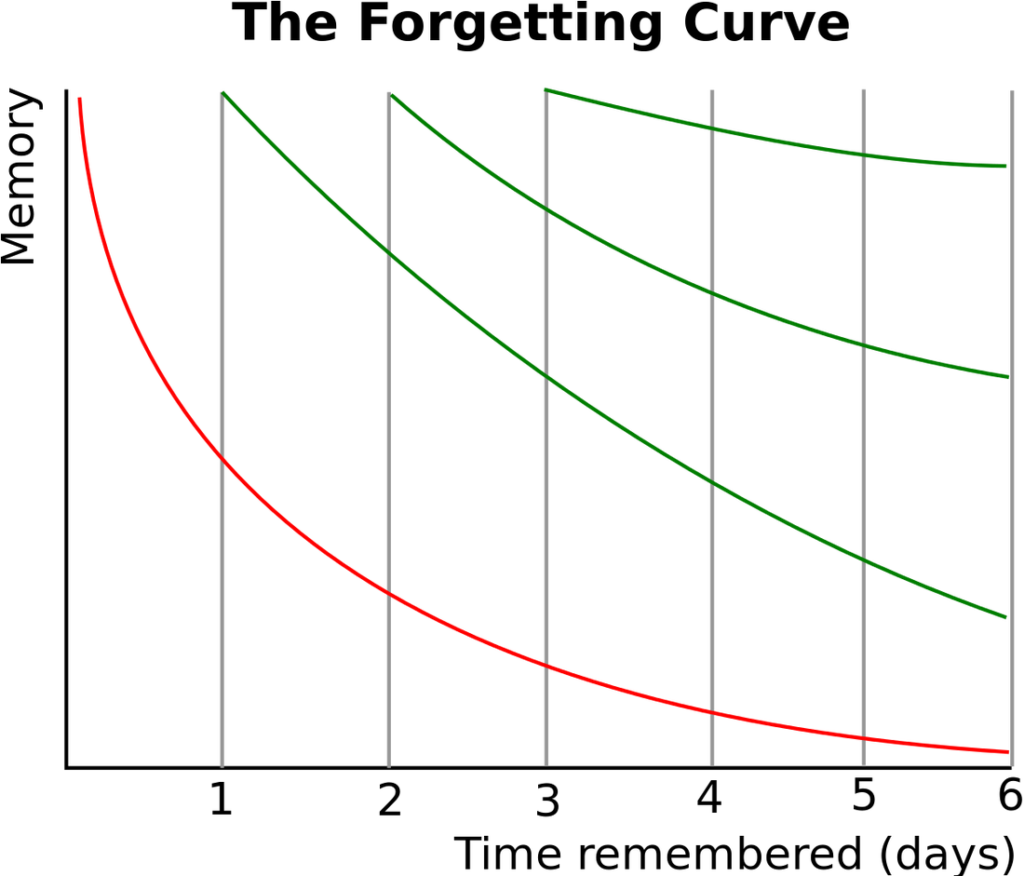
Spaced repetition
If you’re lucky enough to teach a class on consecutive days, they’ve already dropped to under 40% recollection of the previous day’s work. If there’s a weekend in between your lessons, you’re down to around 30%, although the drop-off does decrease as the time period extends. It gives validity to “Miss, I’ve slept since then”, but continued spaced practice is part of beating this curve.
In my mind, there’s no better time to do this than at the start of a lesson. While you’re sorting out who’s forgotten their book and who’s rocking up late, the rest of them can do something meaningful with their time, both in terms of overall progress (which can’t be measured meaningfully over five minutes) and in preparation for the learning they’re about to do, which is almost definitely going to link to what they did last lesson.
Whetting the appetite
Sometimes it’s appropriate to pick a short activity that leads into the learning for the lesson. This could combine with the spaced repetition activity, but might need to be something different. It might explain why the learning for that lesson is particularly relevant to real-life (avoiding pseudo-contexts, of course), or generate a discussion to lead into the main chunk of teaching.
Here are a few examples:
- Starting off a lesson on square numbers by getting pupils to build squares out of linking cubes – this is then a springboard for discussion about why they are called square numbers and links to area;
- Asking the class to think of or bring in examples of percentages in real-life, making the relevance of the topic you’re about to teach clear in their minds.
- Showing a picture for discussion and asking them to identify any maths they can see in it, making sure the topic you’ll be doing is prominently featured – this helps to build links to other strands of mathematics.
A segue into the non-curricular
These are my favourite type of starter. They often get featured on particular dates, such as getting the pupils to sum the numbers from 1 to 100 on Gauss’s birthday, but occasionally I throw things in to keep everyone focused on the point we bother learning maths in the first place – not just to get a grade C (5?) but because it’s such an historically rich, fascinating subject. Let’s face it, the curriculum can end up pretty dry at times, and sometimes a nice puzzle or problem that’s never going to crop up on the syllabus but is interesting and challenging to do keeps me and the pupils awake and enthused.
Unfortunately, I’m really bad at not letting this type of “starter” take over my entire lesson. I once ended up teaching Year 7 about radians instead of doing whatever we were supposed to be doing on Pi Day, due to a great discussion we were having about the number of degrees in a circle, and I gave up trying to fit Fermat’s Last Theorem into a starter and just planned a whole lesson around it instead. But never mind, there’s always the next lesson!
