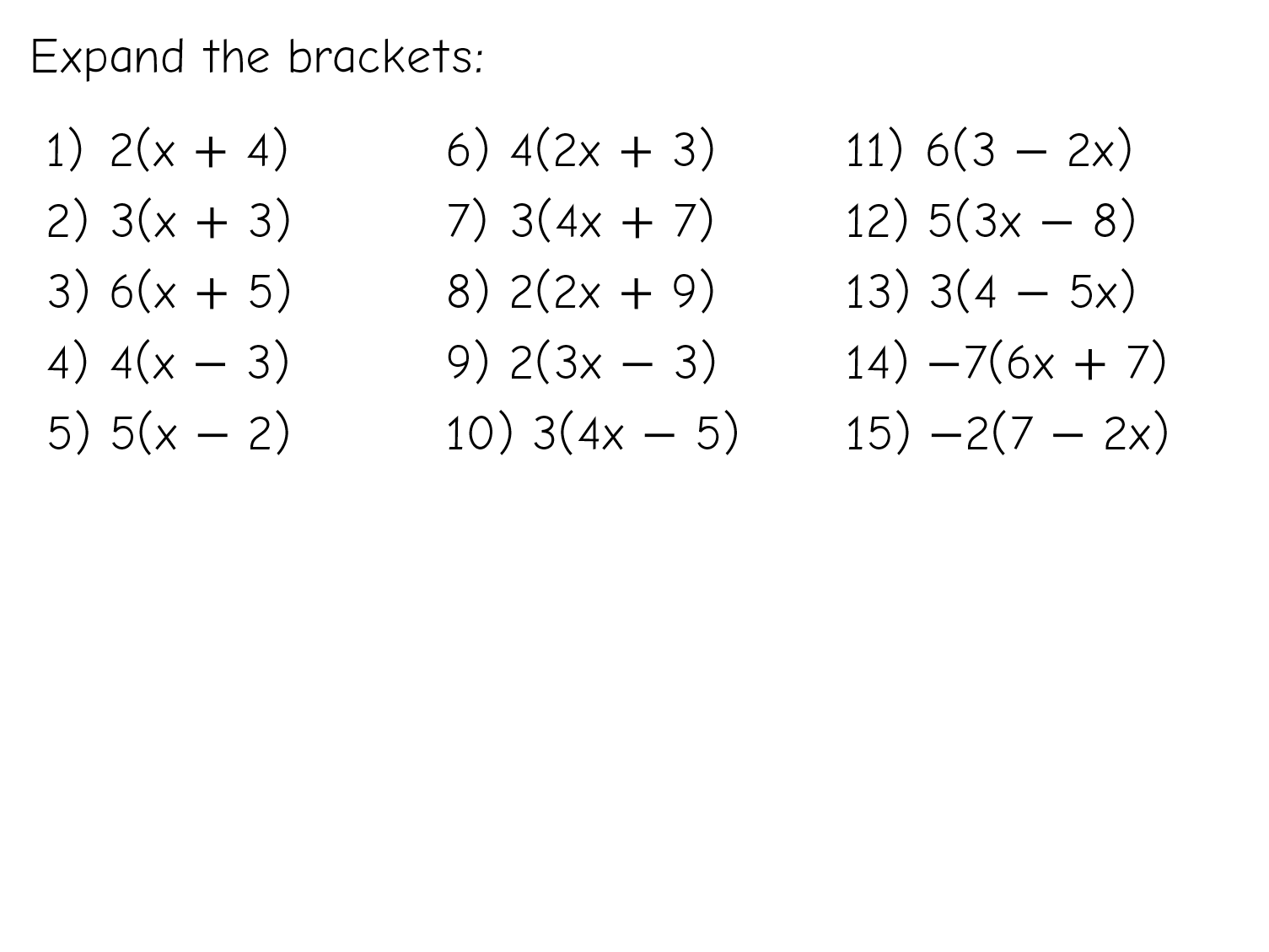Using algebra tiles to model expanding single brackets is really useful because learners can physically count out the required number of groups. There’s something fairly intuitive about brackets representing multiplication when you see the contents of the bracket represented as tiles rather than just algebraic terms.
Introducing expanding brackets using algebra tiles
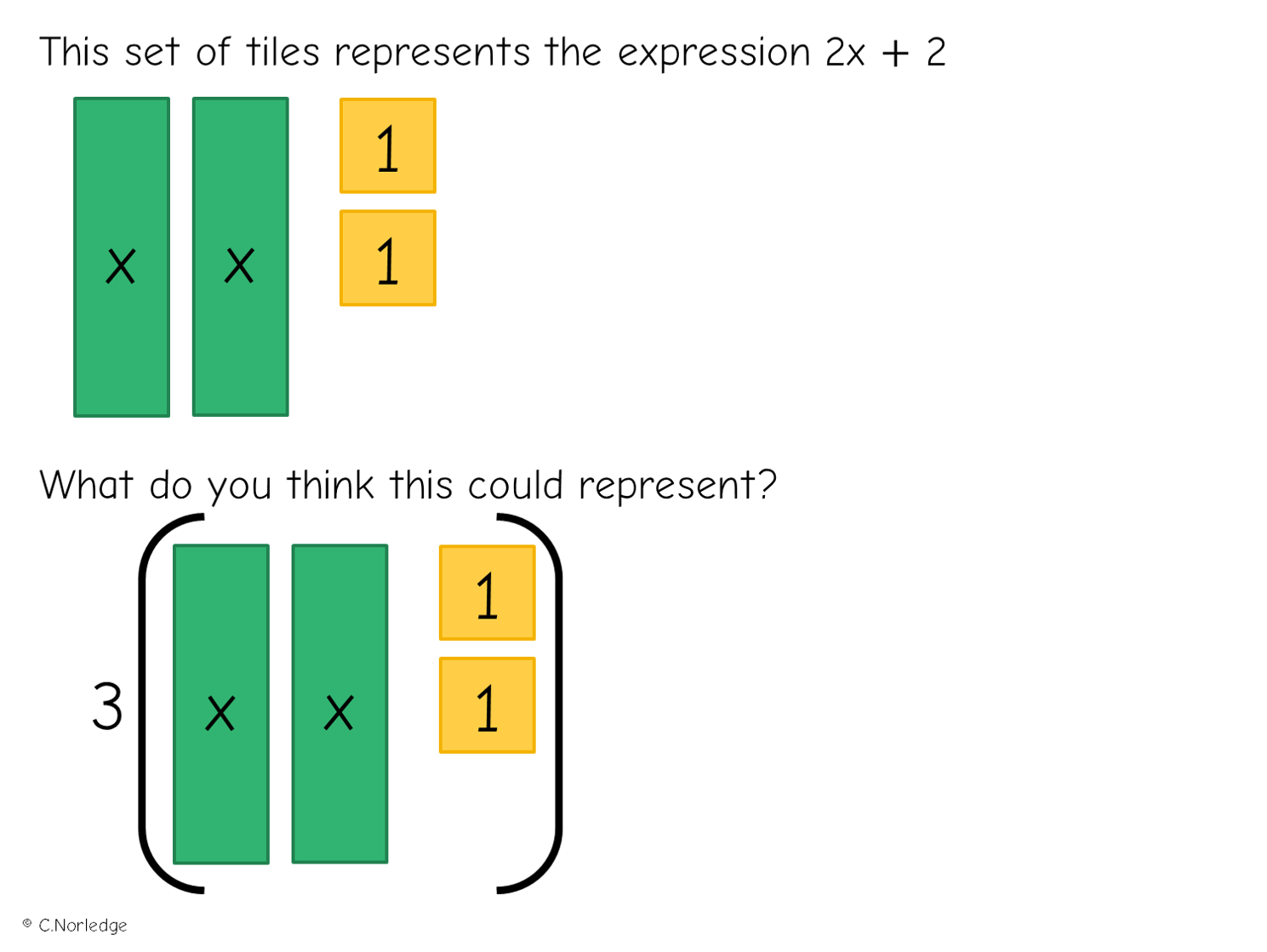
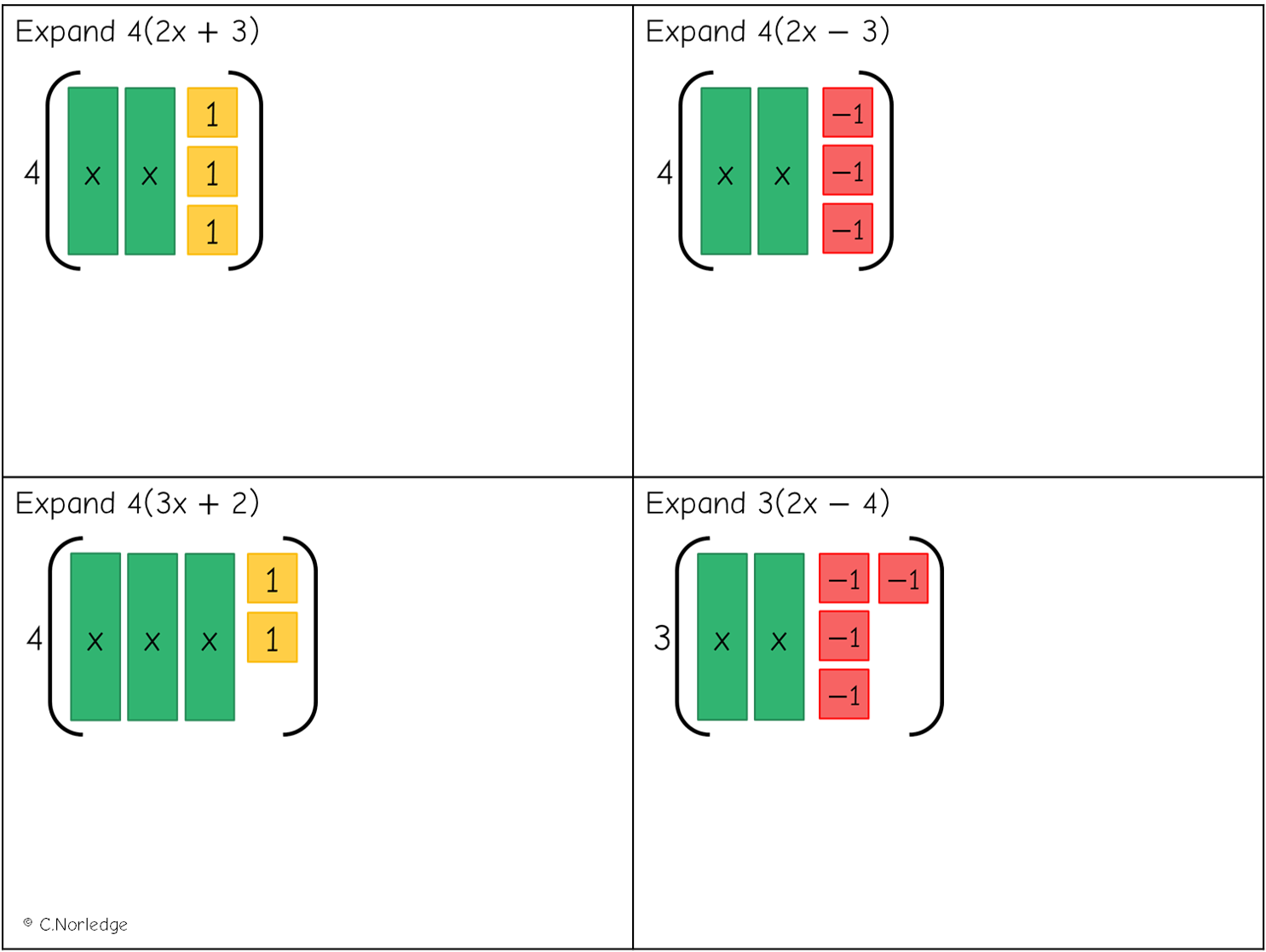
So to start with, we’re just getting used to the notation:
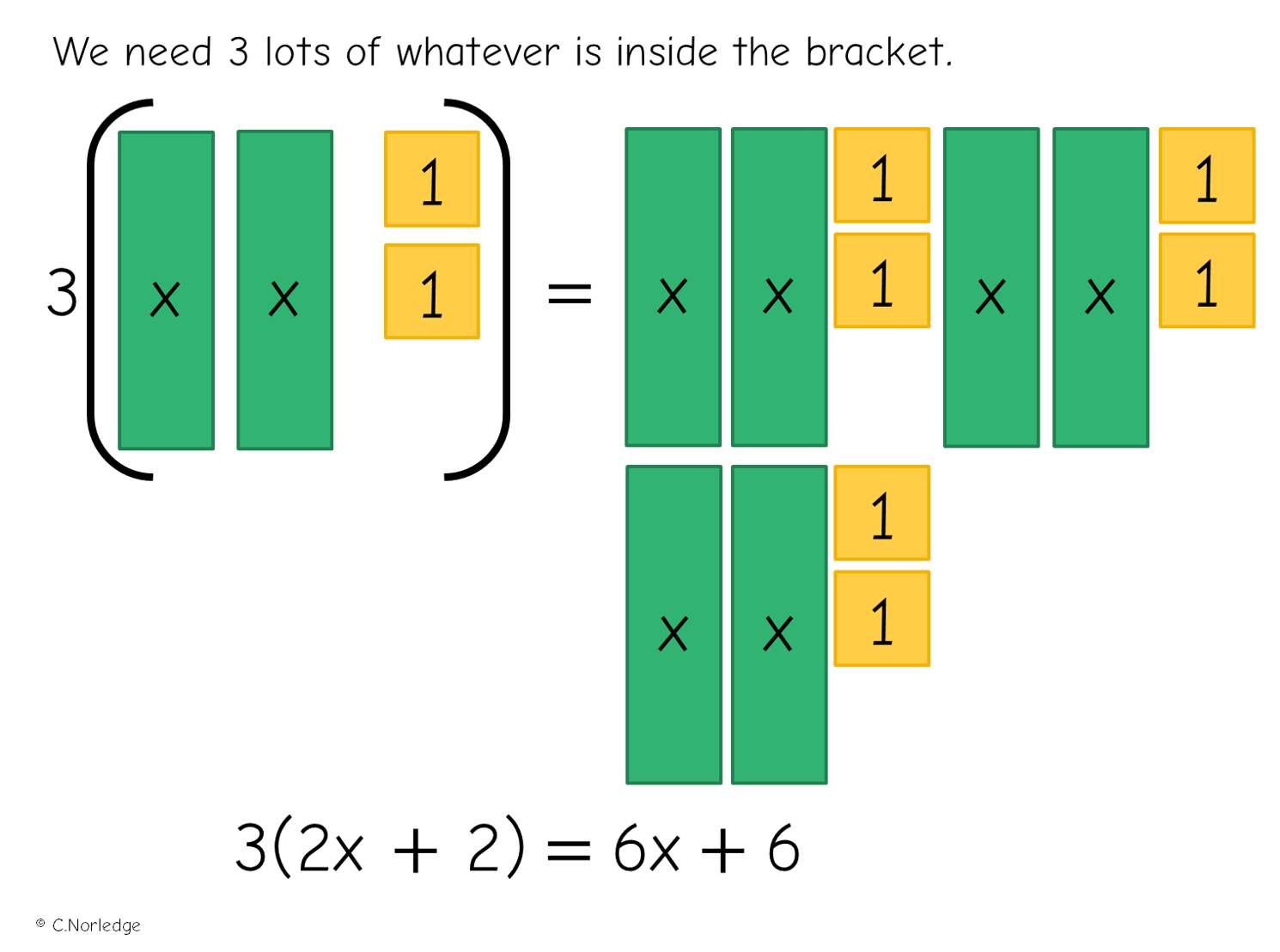
A nice thing about using algebra tiles for expanding single brackets is that learners are much less likely to forget to multiply the end term by the term outside the bracket!
This topic is an area where virtual manipulatives nearly trump the physical for me – so plenty more to look at on the MathsBot algebra tiles manipulative, which lets you create a group of tiles and then just duplicate that group as many times as you need.
Next, an example-problem pair:
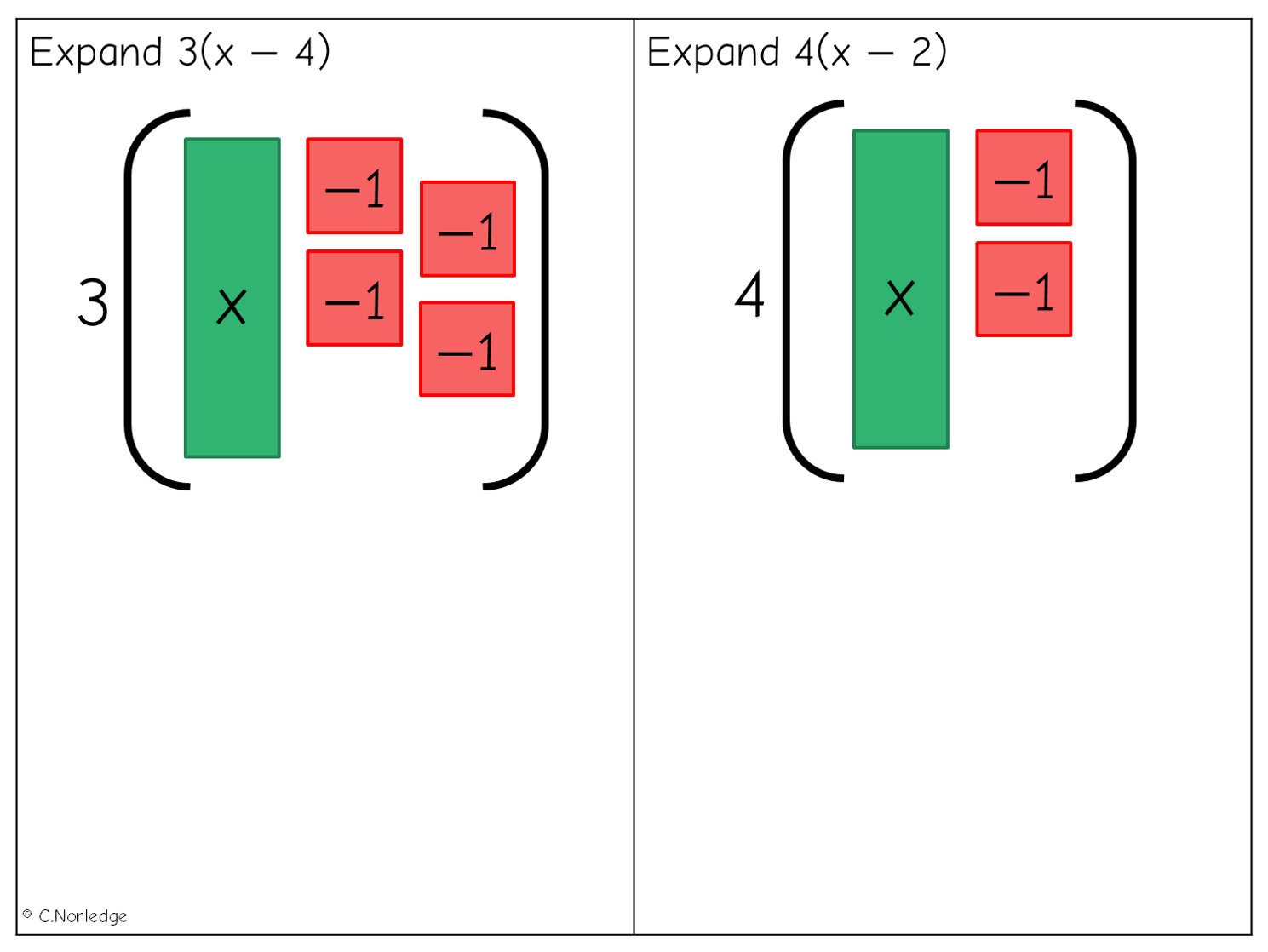
A quick note on using negative tiles – I think they’re fantastic when solving equations for modelling creation of zero pairs, but I tend to avoid them in most cases when working with area models with algebra tiles. But then the examples above ‘feel’ OK to me, because we’re not yet placing these tiles into a rectangle and representing an area.
And then a few more to try…
Depending on the group and how we’d got on so far, I might give them a version of the above without the tiles pre-drawn, or with only some examples pre-drawn – and again, MathsBot all the way for modelling.
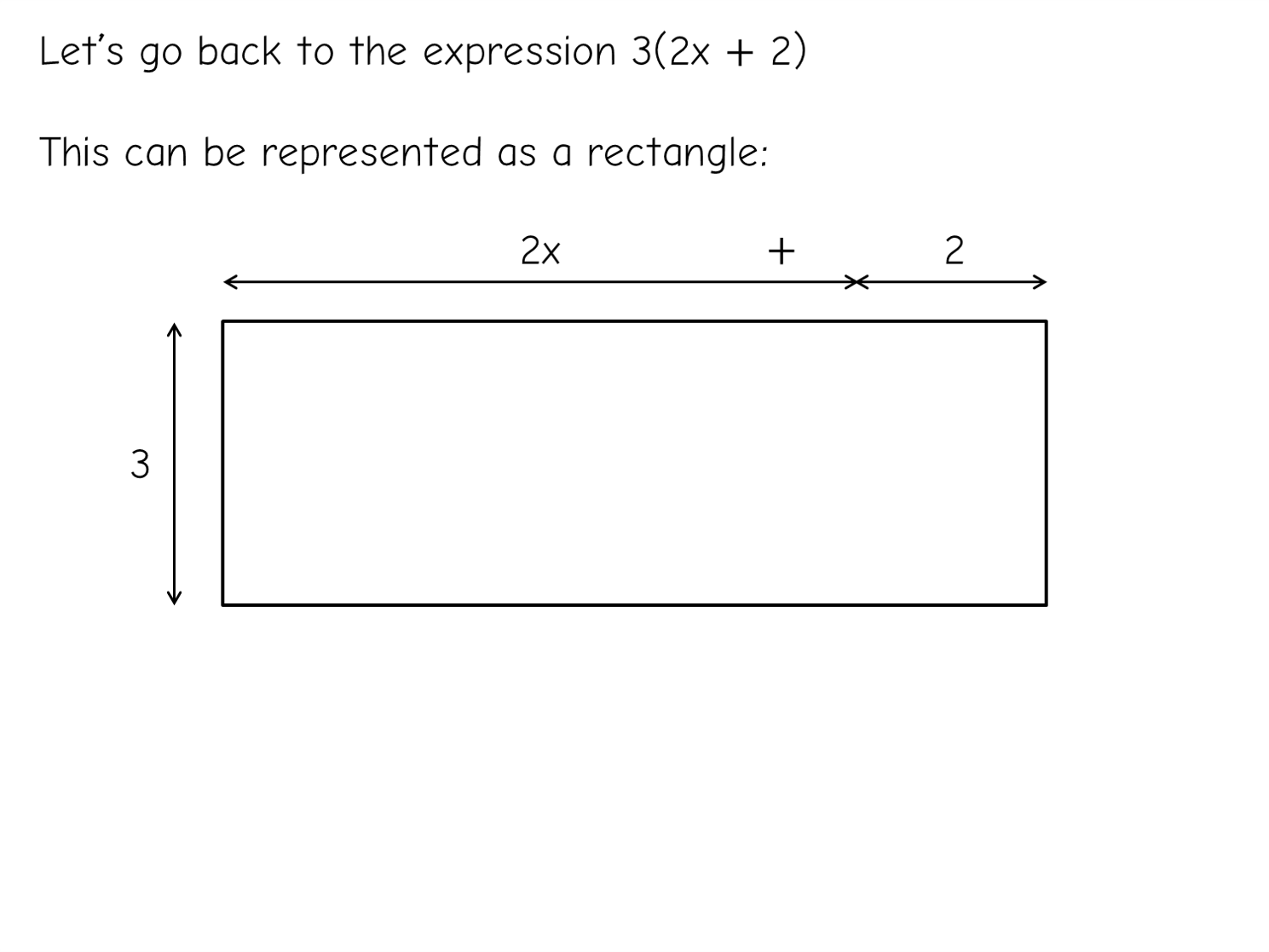
Moving towards an area model
The next conceptual leap forward is moving away from algebra tiles and towards an area/grid multiplication model (before ditching the structures altogether for most learners). This is where I find negative tiles a bit conceptually problematic, so I tend to stick to positive terms for concept development:
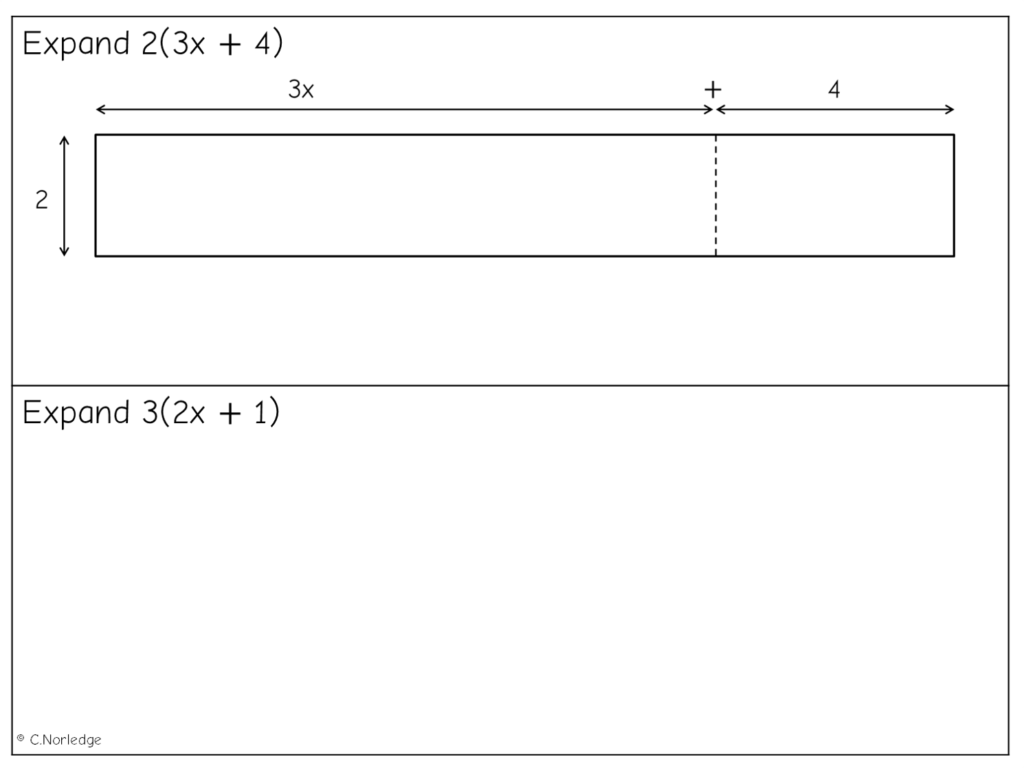
And another example-problem pair:
From area to grid...
And then we gradually begin to reduce the reliance on the model:

As learners work through more of these, they realise that they don’t need to worry about scaling their diagrams to make sure that the 2x bit is exactly the length of 2 x tiles. Then it becomes “do I have to fill in all the tiles, I know there are going to be 8 x tiles in the first box, can I just write 8x?”
Gradually learners move themselves towards a grid-type method – they might need pushing a bit, but generally anything that’s a shortcut or doesn’t involve drawing piles of tiles out is well received!
Practice exercise
Finally, a quick exercise to tackle any way desired – the numbers are small enough to work with algebra tiles if necessary.