This is part of a series of blogs on my favourite way to teach adding and subtracting fractions in a way that sticks and really develops understanding of the process.
Lesson 2 – The importance of equal-sized bars
At the start of the next lesson, present pupils with two more sets of data, this time comparing two groups of unequal size. Using group sizes of 20 and 30 are particularly effective.
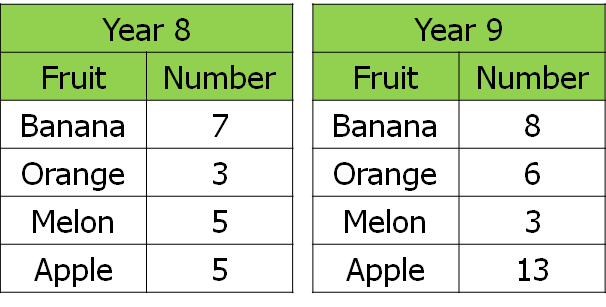
I usually get the class to first represent both sets of data on two more bar diagrams using the template from the previous lesson and get them to record the fractions of Year 8s and 9s that preferred each fruit, cancelling down to the simplest form.

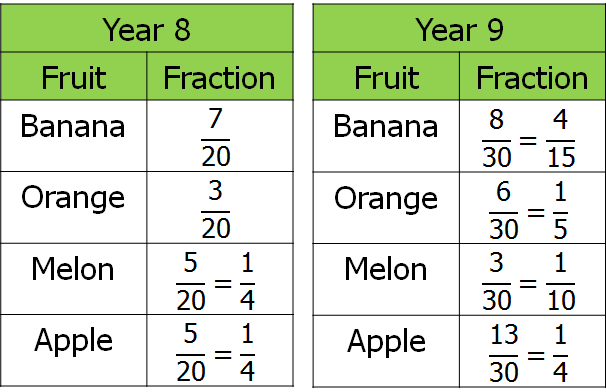
I then ask something like “are oranges more popular in Year 8 or Year 9?” and get pupils to discuss this idea in pairs for a couple of minutes, then share as a whole class. Pupils come up with some interesting points at this stage, and it’s useful to have a discussion about what the numerator and denominator of each fraction tells us. I get them to think about making a comparison and why it’s a problem to compare two bars of different sizes.
Eventually, someone will come up with the idea of using equal sized bars, and they usually spot that the most sensible number to use here is 60. We’re starting to develop the idea of common denominators, although I’m not using that language at this stage. They then draw the equal bars and produce the fractions tables again.
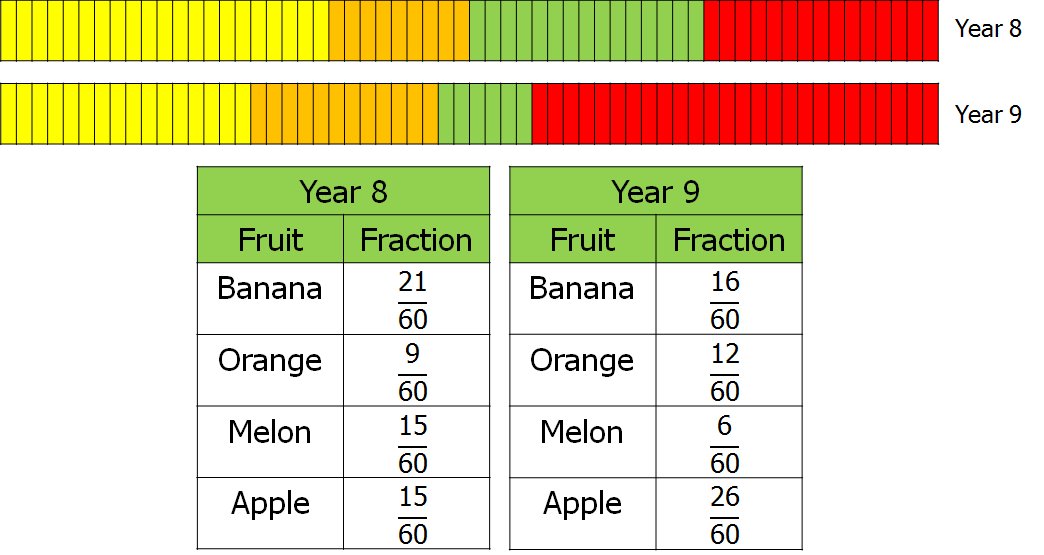
Usually, the rest of this lesson is then spent working on questions like:
- What is the difference between the number of pupils who liked bananas in Year 8 and 9?
- How many pupils in Year 9 liked either oranges or melons?
These develop the ideas of adding and subtracting as totals or differences, allow pupils to compare these amounts on a bar, and reinforce the idea that you don’t add the denominators.
Depending on how I feel pupils’ understanding is developing, I might then give them another set of data such as this one:
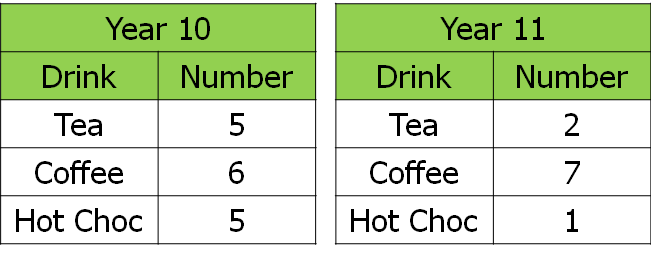
I get them to suggest possible bar lengths for Year 10 and 11, and a bar length that could be used to compare the two. If I feel they need more practice working with concrete examples, I get them to draw their own bars using the squares in their exercise books, and make similar comparisons.
Something that’s really important when working on lessons or tasks which enhance understanding is not to push too hard at a final goal, but to assess and allow pupils to develop at a rate appropriate for them. Occasionally I have left this next step to the next lesson, set it as homework, or (with pupils whose understanding is developing quickly), ask them to do this straight away without bars.
