I started writing about multiplication methods yesterday (read Part 1 here), but waffled for rather longer than necessary, and as a result, didn’t actually get to discuss what I originally wanted to, namely which from grid, lattice (Gelosia, Chinese, Napier’s etc) or long multiplication we should be teaching as a method to pupils.
In one of those weird twists of coincidence, I went on some subject leader training today run by Sheila Eastwood, and we ended up discussing – you guessed it – exactly what I blogged about yesterday, and how this fits in with the idea of mastery in mathematics. We pretty much concluded as I did yesterday; at the moment, no-one really knows what will be allowable as a method on the new GCSE papers.
So in my follow-up post, I thought I’d look at pros and cons of all three methods on the assumption that pupils are allowed to use any in the new GCSE exams, and then consider implications for only allowing long multiplication at the end. Any claims I’m making here are backed up by absolutely no proper research and are mostly anecdotes from my classroom, but I can’t seem to find much independent research on multiplication methods.
1. Grid
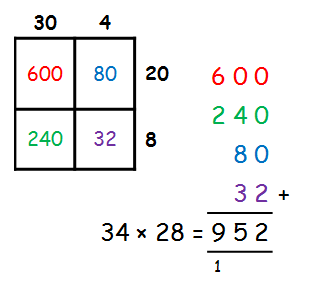
Pros
- Clearest in terms of understanding – pupils can clearly see the place value of each digit, and are reminded that the 3 is actually 3 tens (and so on).
- Most intuitive representation to link multiplication to arrays and area.
- Excellent for developing understanding of expanding algebraic brackets, especially quadratics.
- Easier to find arithmetical errors in calculations than in long multiplication.
Cons
- Least efficient of the three methods – I experimented with Year 8 after looking at all three methods by splitting the class in three and getting each group to do the same calculation using a different method. Those using grid were significantly slower than those using lattice or long multiplication, particularly on questions beyond a simple 2 by 2 digit multiplication.
- Very messy beyond 2 x 2; some pupils struggle with lining up the addition correctly or make arithmetical errors adding up the totals.
Conclusion: Very useful in developing understanding of multiplication calculations and has lots of applications to further work. Should be taught first, but not relied on as a final method due to inefficiency and unreliability with larger numbers.
2. Lattice
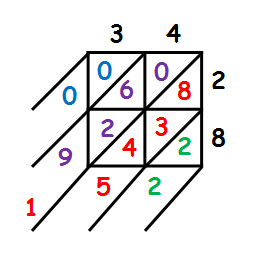
Pros
- No need to worry about multiplying by 10 or 100 and the number of zeroes, eliminating any arithmetical errors creeping in that way.
- More efficient than the grid method, and comparable with long multiplication in terms of the time it takes proficient pupils to complete a calculation.
- Transfers to multiplying decimals (unlike grid method).Errors can be easily identified.
Cons
- Understanding is less transparent than in the grid method.
- Drawing the diagonal lines can be a stumbling block for many pupils.
- Pupils can forget about carried digits.
Conclusion: Its efficiency over the grid method for speed and limitations for error mean that I think all pupils should be pushed towards this after understanding has been embedded. I’ve also seen far more pupils work accurately with this than with the traditional long multiplication algorithm, and there is more scope for checking any arithmetical errors easily. Personally, I think it’s fine for pupils to continue to use this up to GCSE if they are comfortable with it.
3. Long multiplication
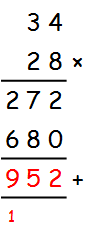
Pros
- More efficient than the grid method; seems to have a slight edge over lattice for multi-digit by single-digit, but time gains drop off for two multi-digit problems.
- Working out is “neater” and easier to organise.
- Pupils don’t have to draw a grid out.Reinforces traditional addition strategies and carrying.
- Transfers fairly easily to decimal multiplication.
Cons
- Prone to errors when pupils forget to “add another zero” when moving down to the next row.
- Very limited conceptual understanding if taught as the only method.Can be incredibly difficult to check multiplication errors in intermediate steps.
- Requires pupils to hold much more in their heads and remember which stage of the calculation they are at throughout.
Conclusion: I don’t have an issue with pupils in my classes using this if they are doing so accurately every single time. For some pupils, it seems to click and that is how they always do multiplications. However, I’ve seen so many pupils repeatedly make errors with this way that I’m not convinced that spending a lot of teaching time on this at secondary level is particularly effective. With GCSE as our main goal (because, let’s face it, with a phone in your pocket, you’re never going to do a scribbled calculation after you leave school), I’d personally be happy with pupils continuing to use lattice multiplication all the way through. One thing I really really hope doesn’t happen is that primaries (and secondaries, if applicable, when we finally get proper answers about the SAMs) stop teaching the grid method because it doesn’t get the pupils method marks. If we’re thinking about deepening understanding and securing mastery, I can’t see how this could possibly be done by just teaching long multiplication. I think you could almost see the three methods as a progression; pupils should start with the grid method, as this links well to the multiplication facts they already know and maintains a (general) pictoral representation of area. They then move on to lattice and some may stop there, which in my opinion is fine – I’d rather have a pupil be able to use that accurately and maybe lose 30 seconds in terms of efficiency than muck up long multiplication repeatedly. Those who want to could then progress to long multiplication, but I do wonder if its prestigious status is more to do with hearkening back to the glory days of mathematics on chalkboards with rows of silent children than a critical evaluation of its actual worth.
Besides which, if we’re talking about “traditional” methods, lattice wins hands-down. There’s a good reason it’s got so many different names (Chinese, Napier’s, Gelosia, I even found someone on YouTube calling it “lettuce” the other day…), and that’s because it’s one of the oldest forms of multiplication we have, far pre-dating the apparently historic algorithm favoured in the new primary curriculum.
P.S. A little Googling indicates that at least one person agrees with my stance on lattice – see this blog post on CavMaths.