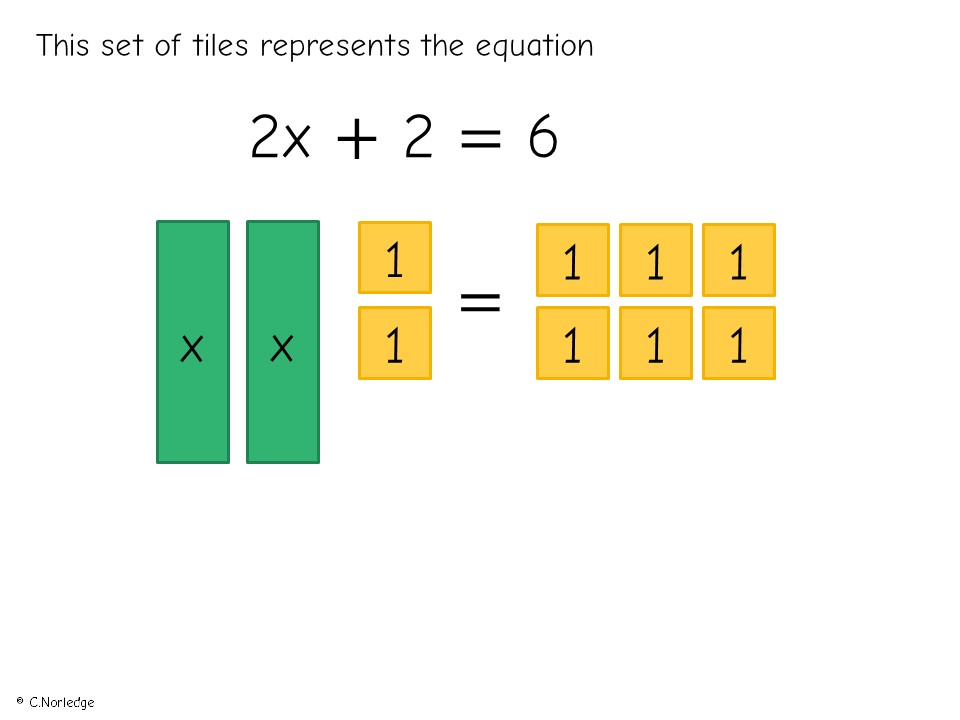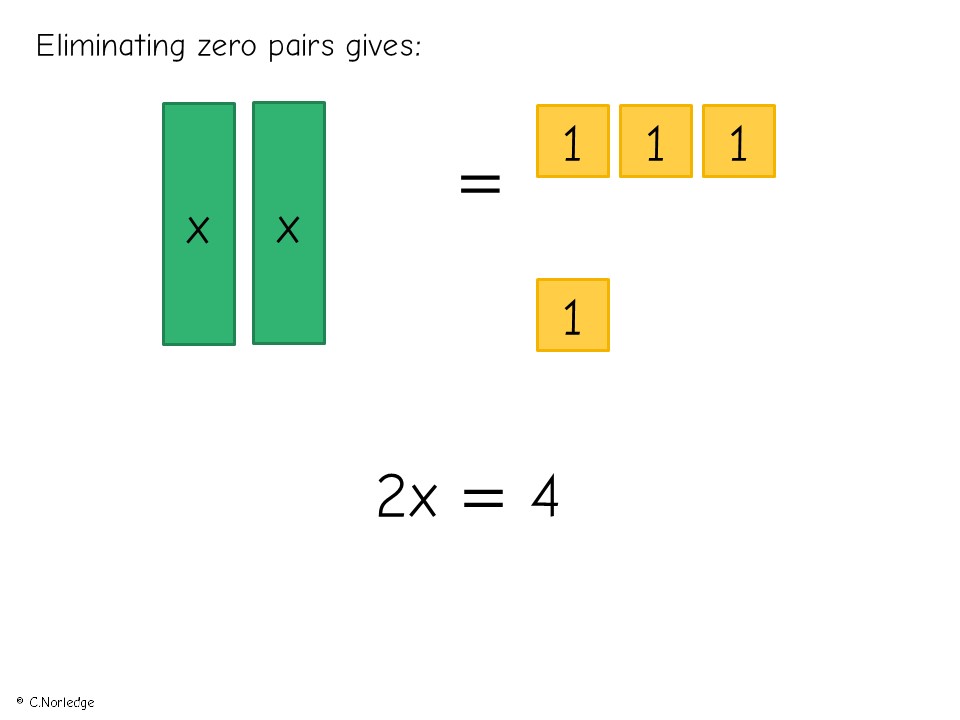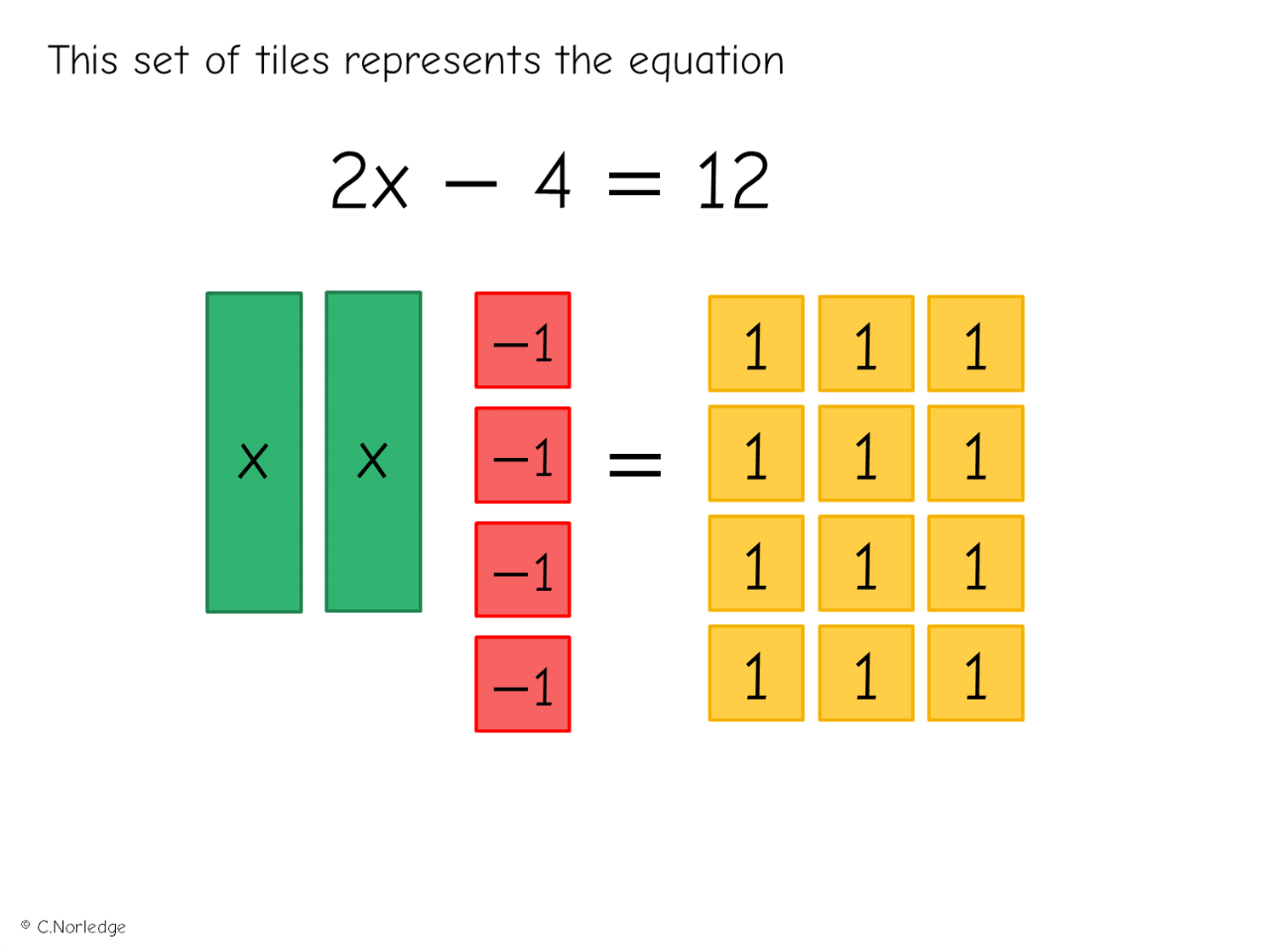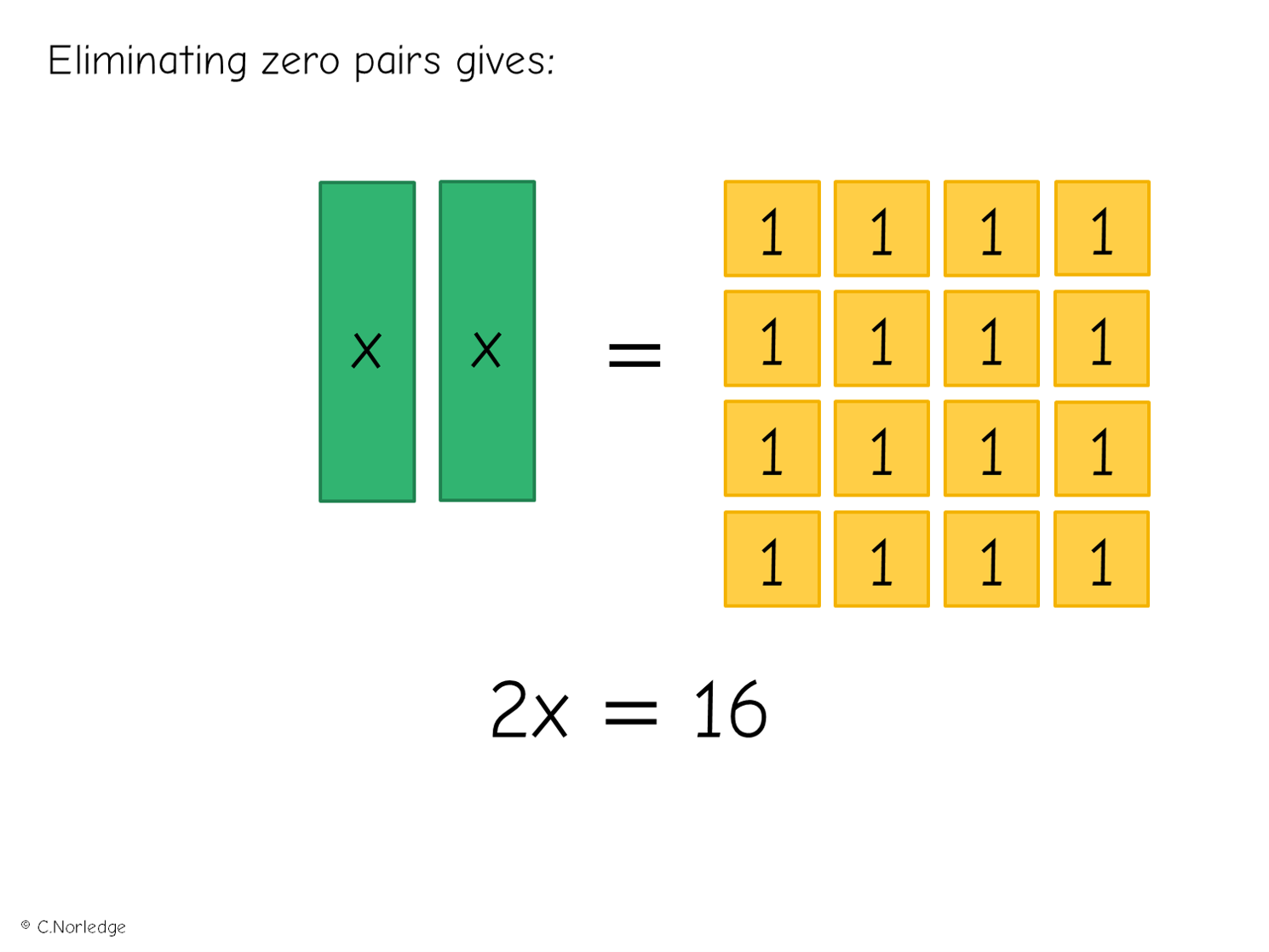- First published March 2015, last updated October 2022
By the time I teach linear equations, I’ve already used algebra tiles quite a lot with learners to create algebraic expressions.
After working through one-step equations and ensuring learners understand the processes involved (rather than just solving “by eye”), I move on to simple two-step linear equations.
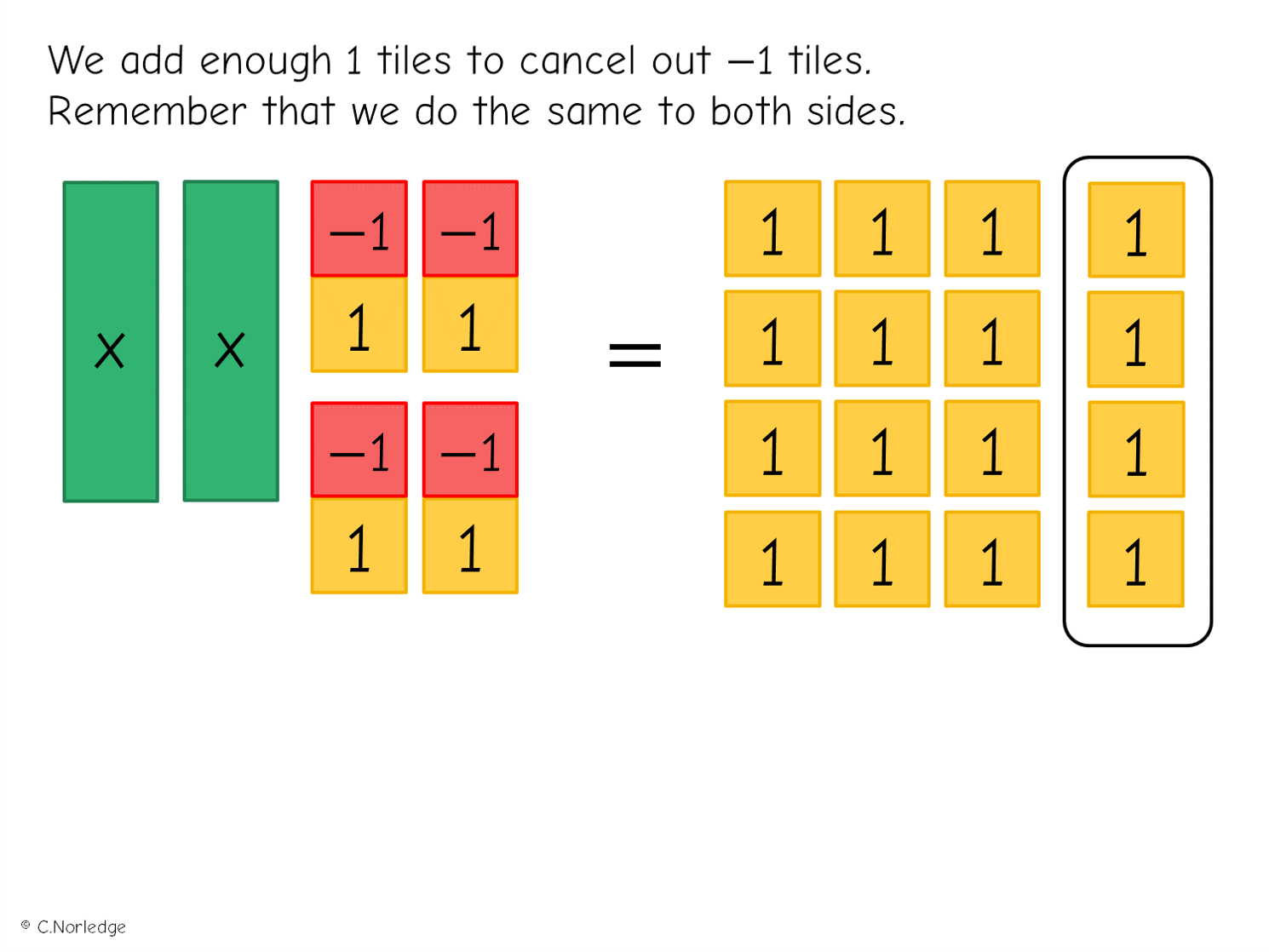
If learners aren’t familiar with the concept of zero pairs from earlier work on equations, or from work with negative numbers, it’s important they understand these concepts before going further.
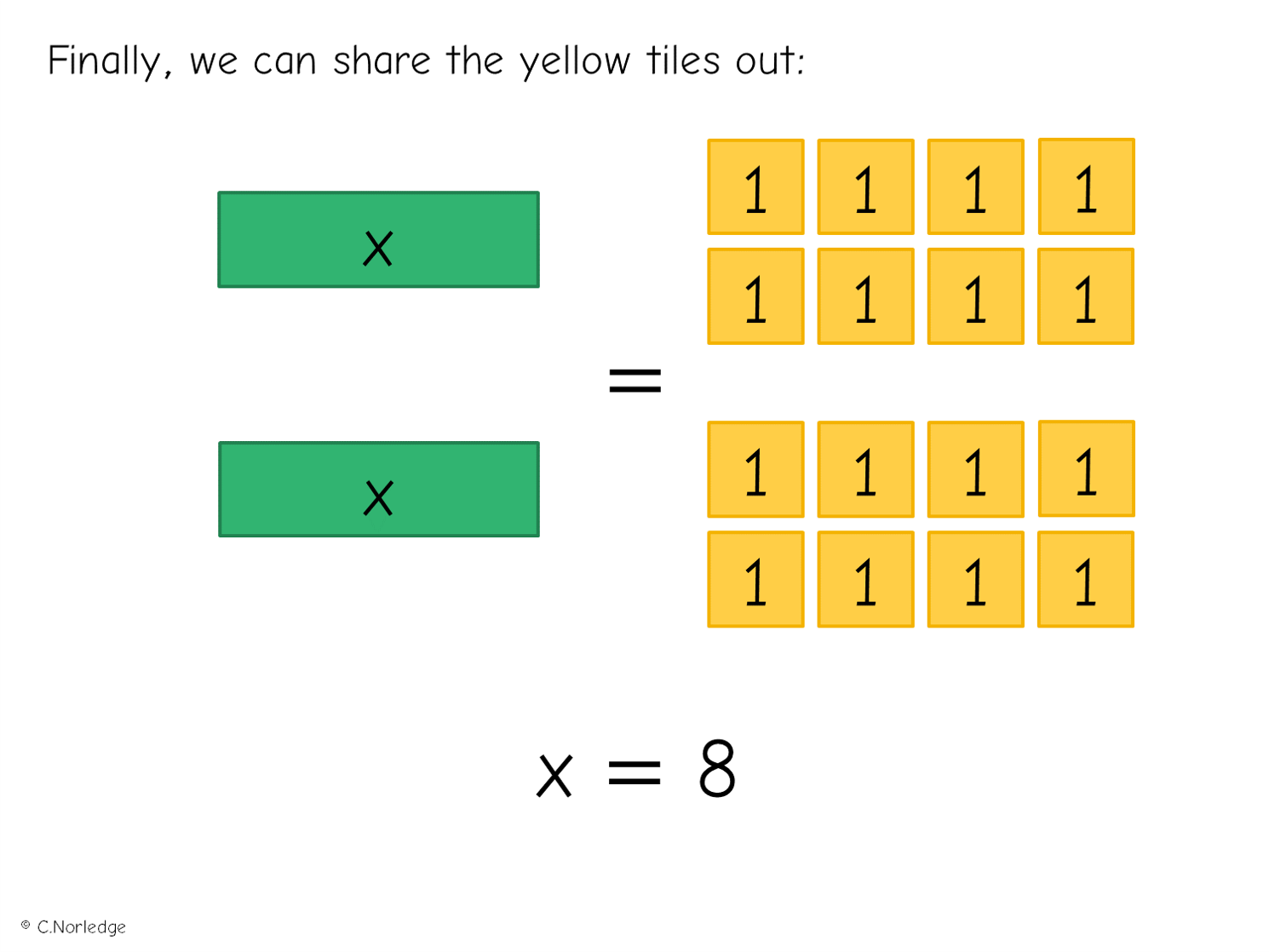
Here’s a straightforward introductory example:
And an example-problem pair (I’d use the MathsBot algebra tiles manipulative to model this).
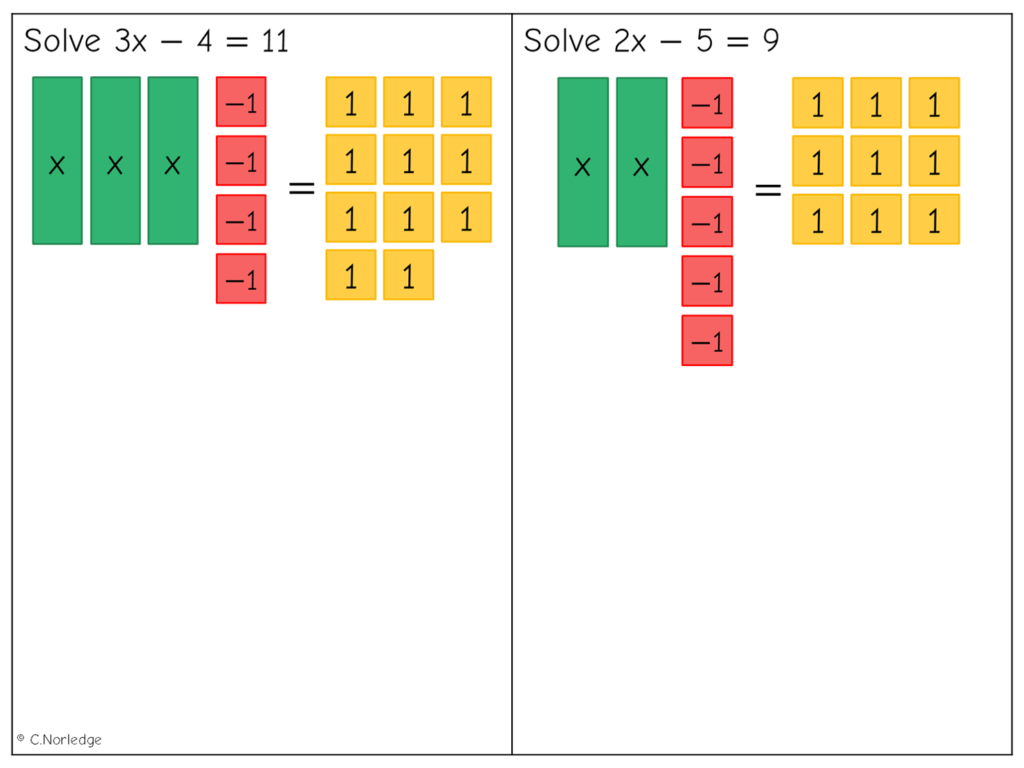
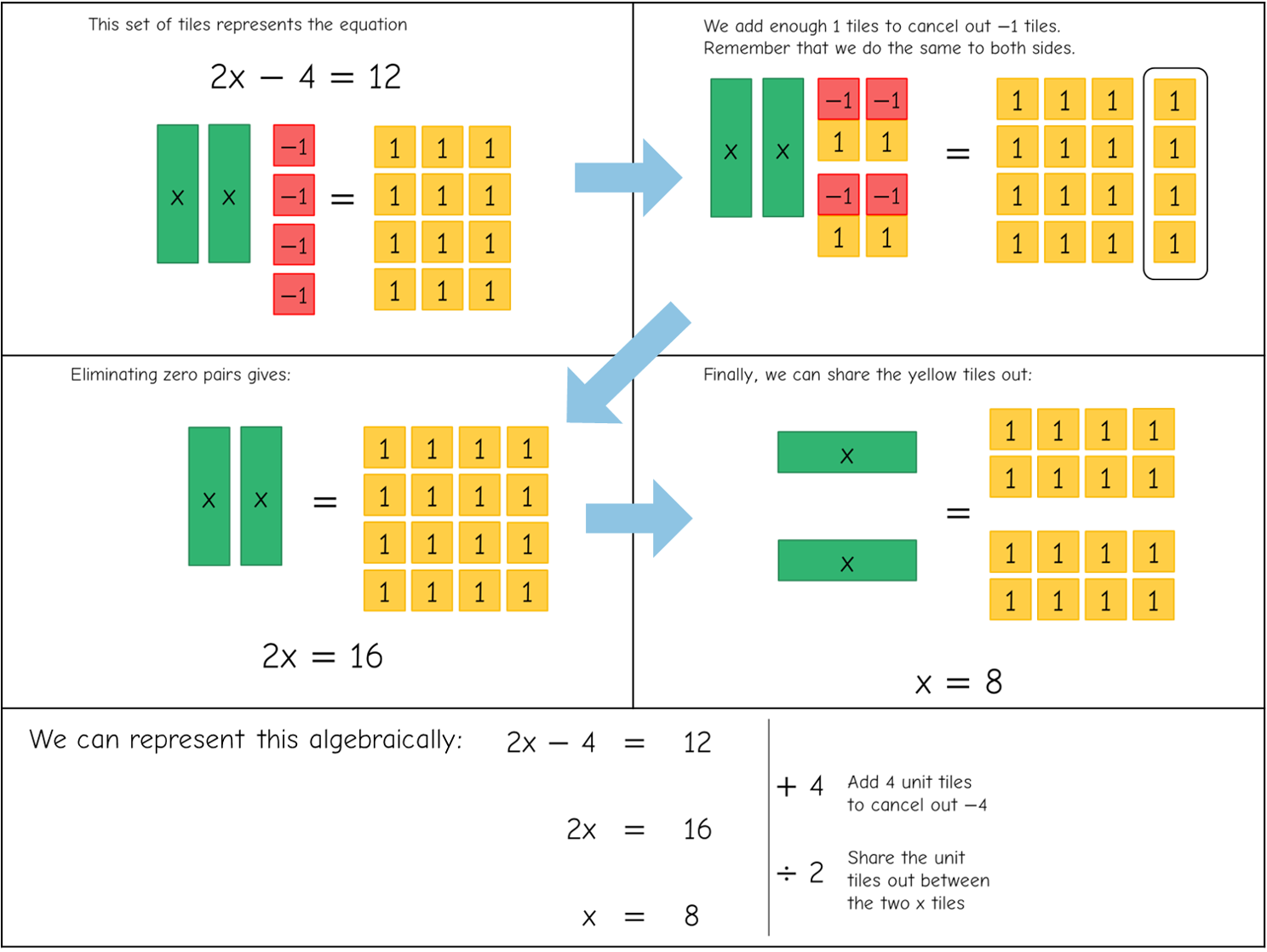
Next, an example involving subtraction of a constant term:
And another example-problem pair:
It’s important to choose an independent practice exercise with sensible numbers when working with algebra tiles – if you’re going to set some problems for learners to practise using the models, smaller numbers are better, particularly if learners are working with physical tiles (virtual manipulatives are better at quickly duplicating large numbers of tiles!).
I also tend to teach solving linear inequalities at the same time, as it helps pupils see the connection between the two topics. For some reason, pupils panic at inequalities in exam situations, even though the solving process is identical, and teaching both equations and inequalities at the same time goes some way to avoid this.
One thing that’s crucial when working with manipulatives such as algebra tiles is that pupils also develop ways of working with correct algebraic notation. When I teach this lesson, while I get pupils to use the tiles to model and demonstrate their calculations, I also ask them to record their working “traditionally” in their exercise books, reinforcing the move away from the tiles to a pure algebraic solution.
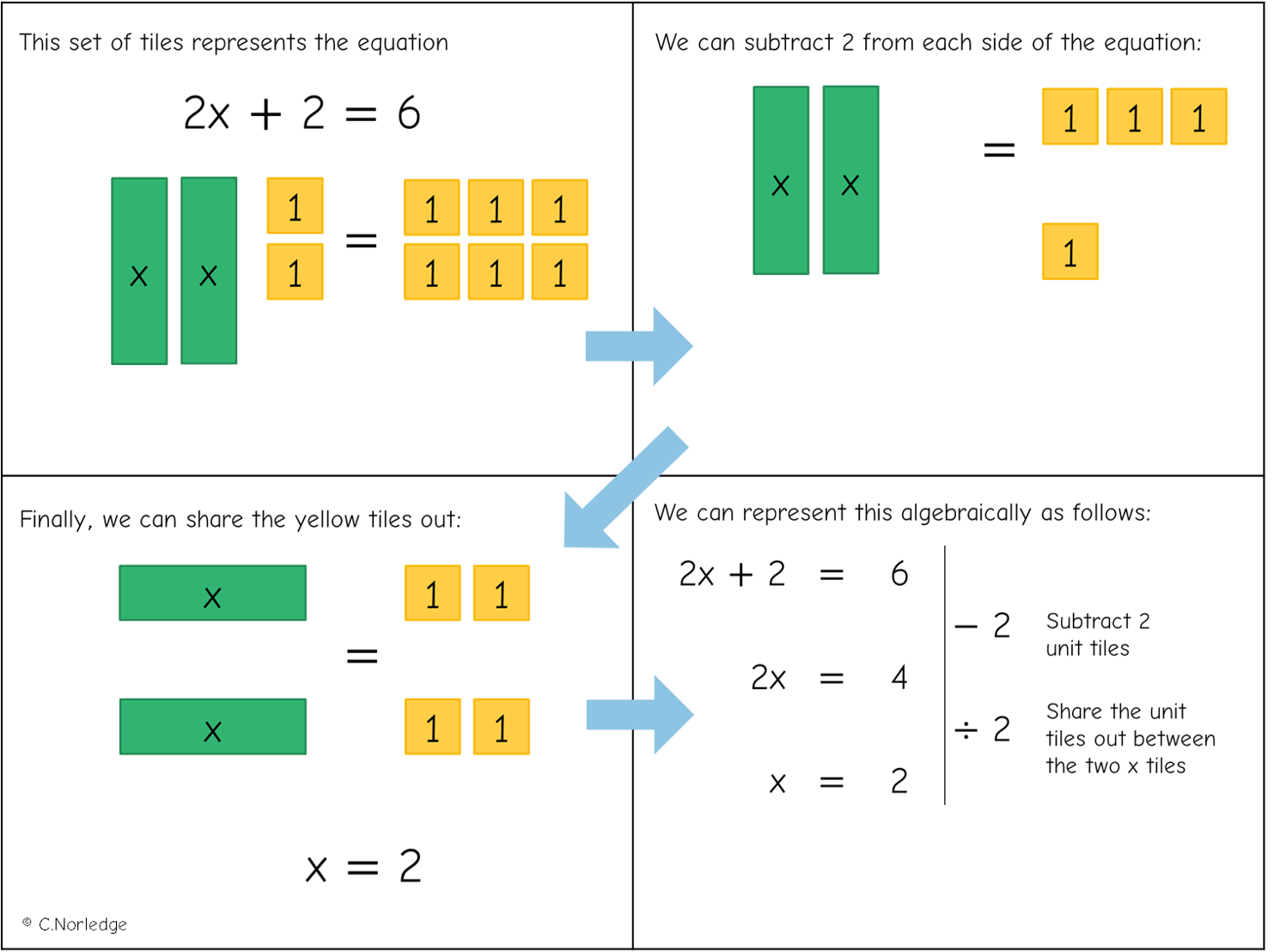
Finally, here are a couple of summary sheets with the examples above: