Factorising quadratics is one of those topics that, for some reason, students just don’t seem to get. I always teach factorising straight after expanding; it seems that students understand the basic principle of “working backwards”, and can even factorise fairly simple quadratics (all positives, of course) pretty quickly and simply. However, I’ve never quite managed to work my way around more difficult quadratics with a > 1 with much success; the students seem to understand what they are trying to do, but really struggle with putting it into practice.
Anyway, last week I went on a training course for the new 9-1 GCSE from Edexcel. All interesting stuff about the exam changes, but my biggest takeaway was this: the “Cross Method” for factorising quadratics with a > 1. I was keen to give it a go with Year 10, so after doing some simple quadratics with a = 1 (mostly OK, apart from the usual wrangles with negative numbers and having to unteach negative add negative is positive), we tried a few with a > 1.
I started with my usual “reverse grid method and reason it out” approach; blank stares and confusion. I then showed them the same question using the “Cross Method”. Cue shouts of “oh that’s easy!” and “why did you even show us that first way?!”.
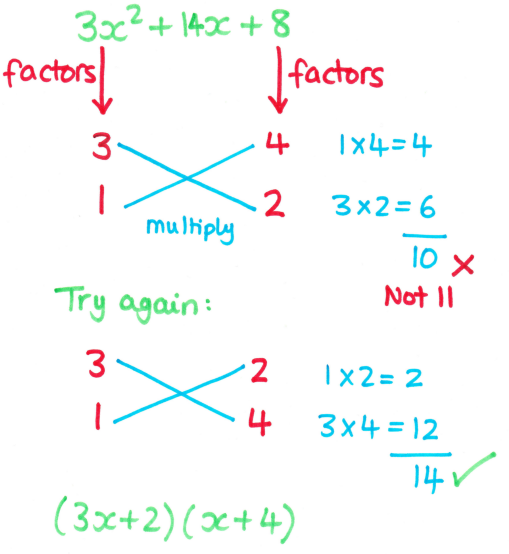
Things I like about this method:
- It’s an easy way into the problem; it turns a complicated quadratic into a little number puzzle.
- It helps students to structure and record their trials. It’s useful for both them and me to be able to see what numbers they have tried.
- It works for all quadratics. I probably wouldn’t encourage this for simple quadratics with a = 1, but it would work!
- It really does help with issues with negative numbers, as students have to do the calculation at the side, which makes them think more carefully about their working.
I think I’ll be using this a lot more in future! It’s not a substitute for understanding, but once the understanding is in place, it provides structure and organisation for the trial and error method.
