This level was undoubtedly one of my favourites when I played the game as a child, and is responsible for many pizza-related sayings in my house. Unlike the previous two levels, this one is not focused at all on Zoombini characteristics. Instead, the player is tasked with creating the perfect pizza for some very picky tree trolls. When each troll has had their pizza made, they move out of the Zoombinis’ way, allowing to group to continue.
Not So Easy
On the first level, players have to create a pizza for a single troll, Arno, from a choice of five different toppings. It’s a little unclear what some of the toppings are, so I’ve taken a best guess at names. To create a pizza, the player selects one or more desired toppings from the machine on the left, then presses the large pizza button at the top. The pizza is transported over Arno, who either flings it on the rock behind him if the pizza is OK but missing something, or in the pit to the front if there’s something on it that he doesn’t approve of. On Not So Easy, the player gets six attempts before Arno starts hitting his pizza-delivery Zoombinis off the screen and back to Zoombini Isle in frustration.
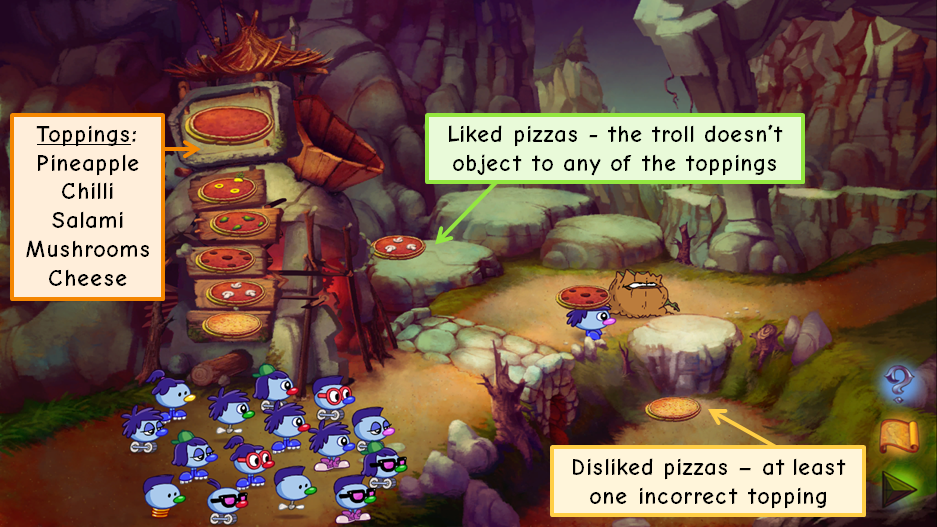
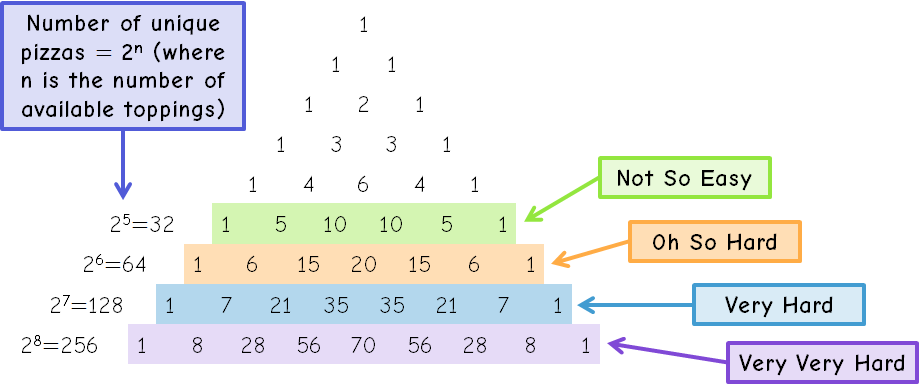
In total, there are 32 possible pizza combinations, which makes pure guesswork an inefficient strategy. However, with six chances before you start to lose Zoombinis, and only one troll to satisfy, it’s a perfectly acceptable approach to produce each of the five single-topping pizzas, judge his reaction to each, and then use your sixth attempt to create the correct combination from this. It’s worth noting that the completely blank pizza also counts as an option – if all five toppings are rejected, the sixth attempt can be used to present the blank pizza.
It’s also OK to introduce a new topping each time. In the example below, once I had figured out that Arno liked mushrooms and salami (but not cheese), I knew that these two ingredients would have to be on his perfect pizza anyway, so included them in my tests of chilli and pineapple.

It might be interesting in a classroom situation to get pupils to consider or even to work out all the possible pizza combinations. This could be done quite easily by listing as here, and could then lead to further discussion about combinations or patterns in Pascal’s Triangle.

Oh So Hard
The next difficulty level introduces an extra troll, Willa, and some extra choices for the pizza machine. Cheese is removed, but is replaced with two ice-cream sundae options, namely sprinkles and a cherry. Essentially, both still function as “pizza toppings”, giving the player a choice of six toppings in total and doubling the number of possible unique pizzas to 64.
As before, the player has sufficient attempts (seven on this difficulty setting) to try each topping on its own, then combine to create both trolls’ perfect pizzas. There is never any overlap between the two trolls – for example, they will never both like mushrooms. However, there is no guarantee that all of the toppings will be used, and the trolls frequently both reject one or two toppings.

Very Hard
The third difficulty level introduces a third troll, Shyler, and cheese appears once again on the pizza machine. A choice of seven toppings now means that there are 128 possible unique pizzas, making guessing correctly nearly impossible. However, with eight pizza attempts before your Zoombinis end up getting smacked around, the tactic of producing single-topping pizzas still works every time.

Once the player has figured out the correct approach, the first three difficulty levels of the Pizza Pass become fairly trivial. The algorithm of “create one of each single topping, then combine” works sufficiently in every case. However, the quirkiness of the trolls and the excellent voice acting mean it doesn’t really get boring to replay.
It’s at Very Very Hard that the puzzle changes subtly, so the algorithmic approach breaks down and alternative tactics are needed. Because of these greater complications, I’ve saved this for a separate post, as this one was getting too long!
Thoughts on Classroom / Educational Use
- Get pupils to work out or list the total number of pizza combinations for each level of difficulty – a great opportunity for some systematic listing and pattern spotting.
- Create Pascal’s Triangle from the pizza choices – explore the link between the number of available toppings and the number of unique pizza combinations.
- Explore different strategies for solving each problem – as yet, I’ve not found a more efficient algorithm than the one described above – but there may be one!