I’ve spent quite a bit of time so far over half term working on the resource areas of my site – one topic I was keen to get a few more resources for was writing algebraic expressions and using correct algebraic notation, as I’m teaching this to Year 7 after half term and my collection was looking a little sparse.
Today I’d also found a link to the Cuisenaire Rods manipulative on the NRich site, which is absolutely fantastic. I remember discovering a dusty old box of rods in the resource cupboard during my NQT year, digging them out and then not really doing anything relevant with them because I didn’t have a) the time or b) the experience to work out how to use them without just confusing the pupils more. I’d always been determined to go back and check them out properly though, particularly with the links to the work I’ve been doing with algebra tiles. Obviously the first thing you can do with them is just use them to illustrate multiplication as repeated addition and get pupils to have a play around writing expressions for these:
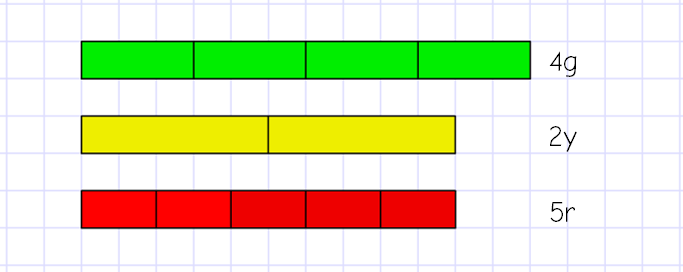
While making these examples, I realised how easy it is to accidentally create equations – from this picture, we have 2y = 5r and a visual link to y = 2½r. Similarly, there’s 2g = 3r, giving g = 1½r. Depending on how comfortable pupils are with fractions and inverse operations, you could delve even further into writing r in terms of y and g – but that’s a blog for another day, I think!
Stacking the blocks one under the other clearly links repeated addition, multiplication and area:
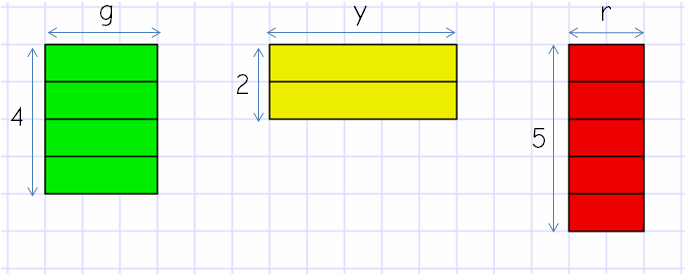
This can then develop easily to multi-rod (variable) expressions:
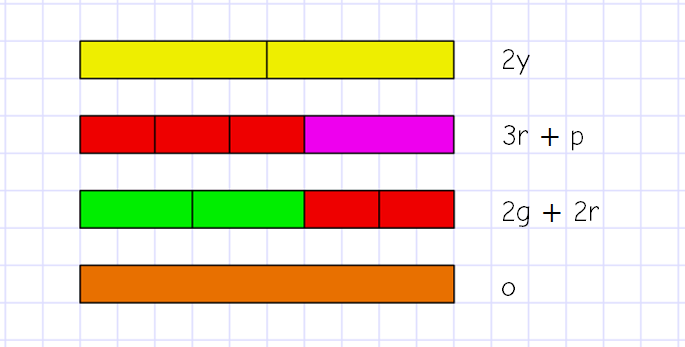
I’ve deliberately picked sets of rods that are 10 long, and I’d envisage that a further discussion about the equations we could make would happen in a classroom situation. Off the top of my head, you can spot 3r = 2g, p = 2r, 2y = o and then other relationships by picking fractions of one amount or another.
Unfortunately, without delving further into work on equations, you can’t really represent subtraction or division. Despite this, I think using the rods might be a great way into a topic that pupils find really difficult – I’d probably have a play with these for a couple of lessons before moving on to algebra tiles and introducing squares.
Also unfortunately, I am no longer at the school with the dusty box of Cuisenaire rods in the stock cupboard, and as far as I know we don’t have any kicking around anywhere at my current place, so I’ll be playing with the manipulative only. However, I am pretty tempted by this funky set of fridge magnets on Amazon…!
EDIT: I’ve now written a resource to test out when I get back to school; I’m probably going to leave the second slide to start with, as I don’t want to muddy the waters by teaching equations and expressions at the same time.
(Image credit: By Celcom, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=9511548)

