I’ve written quite a few posts recently about using ratio tables extensively in my teaching for proportional reasoning. Following the explosion on Twitter about Edexcel’s non-calculator paper last Thursday, I thought it might be time for a critical evaluation on my part of just how useful (or not!) they are in tackling any or all of the proportional reasoning problems on the most recent paper, particularly if we should see this as an indicator of things to come, as @El_Timbre suggested in this brilliant blog post on Sunday.
I’m approaching this from the point of view of pupils aiming for a grade C, as I’ve had borderline groups for the last two years, and no top GCSE sets for about four, due to having plenty of A Level Maths on my timetable already, so I’ll admit that my pedagogy and knowledge of grade A/A* topics at GCSE is fairly limited.
Q1b Percentages from a stem and leaf diagram
I posted about how useful Year 11 found ratio tables for converting fractions to percentages back in May, and I was happy that at least three pupils mentioned to me after their exam that they’d used this strategy on this question to get the correct answer.
I’m still pretty convinced on dealing with fraction to percentage conversions with ratio tables, but I can see that it might be a little unnecessary here. I’d like to think that once pupils had got the fraction 3/20, they would spot that 20 goes into 100 five times and multiply the numerator accordingly.
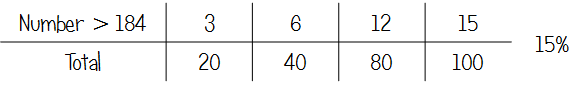
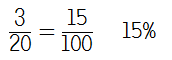
Q4 Plant comparisons
Overall, I thought this was a nice little problem-solving question. It involves pupils working out a percentage, then deducting this from the total cost. Again, I know that most of my groups have found ratio tables useful for structuring their working out, but 20% is a fairly simple percentage, so I can see some pupils not bothering.
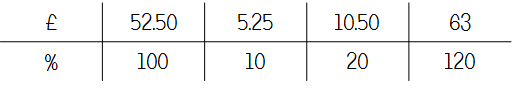
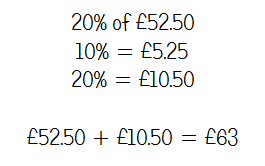
Q9 John’s conference
As the Twitterverse astutely observed, why not get people to bring their own pencils? However, assuming John doesn’t want to put people out, this was a fairly straightforward LCM problem. I quite like the ratio table approach here as it tidies up listing the numbers somewhat, and might avoid any silly errors with miscounting the number of boxes at the end. It also allows pupils to double up to 8 boxes of pens without having to write down each number up to 8 x 15, again eliminating potential for slips in calculations.
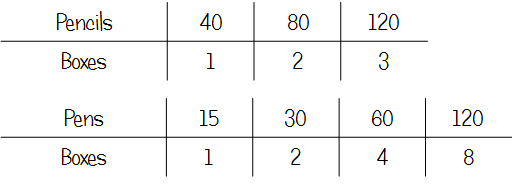
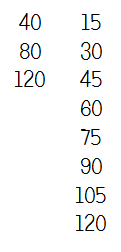
Q10 Mary’s conservatory
I’ve been trying to encourage my Year 11s to scrape every single mark on the Higher paper, and split problem-solving questions where possible. Many of these area/problem solving questions include a percentage calculation that can be done without needing to find the area first.
In a similar vein to the plant comparison question, the only benefit of a ratio table here is structuring working out – I don’t think it adds anything in terms of making the calculation more straightforward.
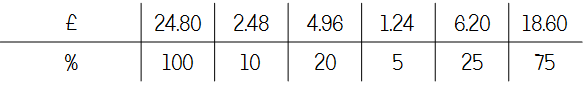
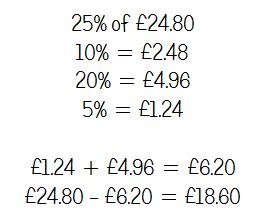
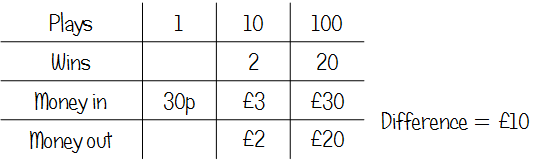
Q11 Karl’s game
Again, a table offers a bit of help in terms of structuring working out here. If pupils get used to constructing these for themselves, it’s conceivable that they’d find this useful to put in what they know, then work out anything else that they can. It might help them to make the link between 10 plays in part (a) and 100 plays in part (b).
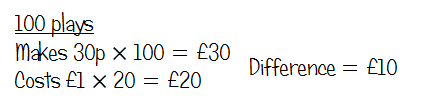
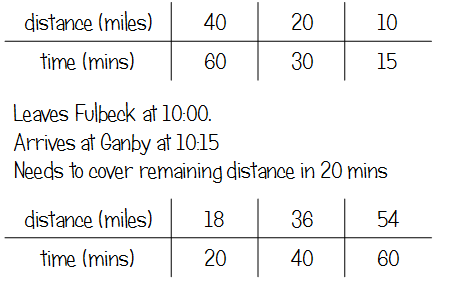
Q14 Raksha’s journey
This is the first question I met that really convinced me that a ratio table was the superior method or way to structure working. From conversations with pupils (and reading on Twitter), I know that those who applied the sdt formula got really confused with units – there needs to be an appreciation that the time is given in minutes but speed given in miles per hour. Structuring using a table kind of avoids these errors in the first part of the calculation, and makes it clearer to see what you need to do in the second part to get an answer in miles per hour.
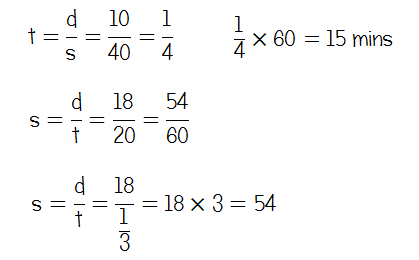
Q15b Does the point lie on the line?
This question pulled me up short a bit – I’ve avoided this with my Year 11s this year in favour of cherry-picking easier marks – but when I was doing the paper, I immediately used the “A Level” formula y – y1 = m(x – x1). I went back and checked over the current and new GCSE syllabi, and finding the equation of a line given two points seems to be listed as new spec only, but, as I said at the top, I have limited experience with teaching A/A* topics and related pedagogy.
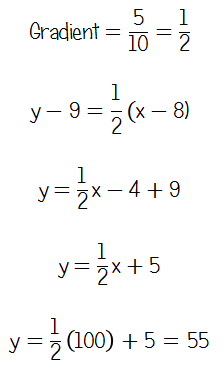
According to this site, it’s a new topic coming to Foundation and Higher, so there are obvious implications for teaching next year.
Chatting to a few pupils in top sets, many of them either found the gradient, then substituted in one point to find the y-intercept, or, overwhelmingly, used a sketch.
A colleague suggested that the approach she had used was getting them to work out the gradient from the two points, then work out if the third point gave the same gradient.
However, I started to think about making this question accessible for borderline pupils who (let’s face it) won’t have as developed algebra skills as those aiming for As or A*s.
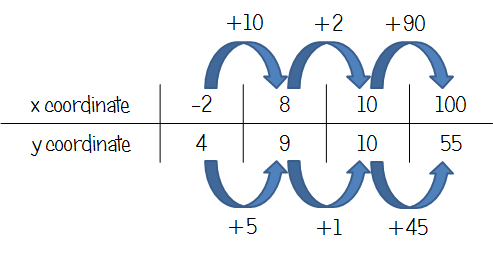
Now, obviously this isn’t really a “ratio” table, as we’ve got a linear relationship, not direct proportion. However, if we look at the change in x and change in y for the two points we’ve been given, it’s clear that the increase in x is double the increase in y.
From here, it’s not too difficult to get from 8 to 10 and then 10 to 100 with the x coordinates, resulting in a y coordinate of 55, proving that the point (100, 56) is not on the line.
Whether or not this is an acceptable way to “show how you work out your answer” remains to be seen!
I’m not meaning this to be a passionate argument for the use of ratio tables – they work really well with some pupils for basic percentage calculations, and (I think) have stopped some of mine from just panicking in an exam and working out “something”, then going from there. I think use for SDT and DMV may prove really useful, particularly for those that struggle to rearrange formulae.
What do you think? Drop me a comment below!