I absolutely love teaching Pythagoras’ theorem – not sure why, but I suspect it has something to do with the sense of “wow” I got when I first learned about it and realised that maths isn’t all about doing sums. There’s loads of really interesting stuff you can do with it, and as the first real theorem that most pupils will meet, I think it’s worth doing it justice.
1. Discover the theorem
My favourite way to introduce Pythagoras’ theorem happens to also be the first lesson I ever taught – before I even got a GTP place and to a group of (then) very scary looking Year 11 boys. I think it has a special place in my heart for that reason, but it seems to work well, so I drag it out every year. It takes a bit of preparation, but is well worth doing. I’ll add that this idea isn’t my own, and was shamelessly pinched from a fantastic teacher I had the joy of observing and working with for two weeks on the Students Associate scheme when it was still running.
You need a selection of pre-drawn triangles and squares on centimetre paper. Include the typical 3, 4, 5 and 6, 8, 10 triangles, but some simple ones with half-units also work quite well. You also need a large piece of paper (two sheets of A3 stuck together does the trick) and glue for each pair or group. Alternatively, follow the links to download my version.
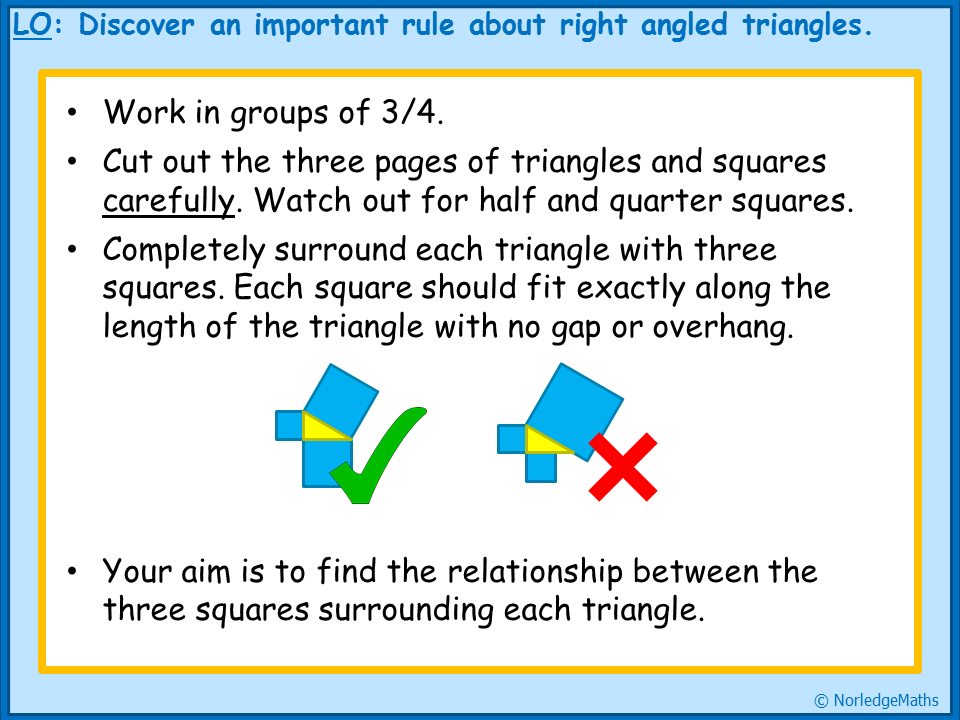
Give the pupils the pieces of paper (or cut them out beforehand if you’re feeling generous), with the instruction that they need to completely surround each triangle with three squares. If they are cutting, make sure they do it accurately – I’ve previously had pupils “correct” my squares by cutting the half-squares off the end! It’s worth checking their work carefully before you let them glue it down, as some have a tendency to match up in a “that will do” way, rather than making sure the squares are exactly the right length.
Once they’ve done this, I ask them to work out the area of each square (they can do this by counting or multiplying), then look for a link, annotating on their posters as they go. Towards the end, I pull the class back together and we discuss what we’ve found out. Depending on where I’ve judged their understanding, I’ll go straight to the algebraic representation or leave this for the next lesson.
I also like to tell the pupils a story my dad told me when he taught me Pythagoras’ theorem; I vividly remember sitting in our dining room at home, looking at the square tiles on the floor, and hearing about Pythagoras pacing around the temple in Samos looking at patterns on the floor, and this was how he came up with his theorem.
Obviously, this story has absolutely no historical basis whatsoever, but it works mathematically, so it’ll do for me!
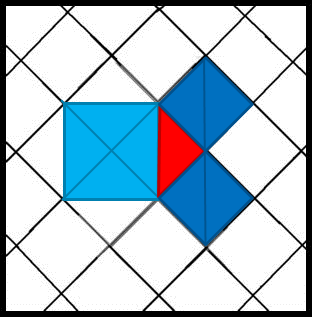
2. Formalise using algebra
I usually then spend some time working on developing and formalising an algebraic approach – I think this is important for embedding algebraic manipulation skills and can avoid issues with whether to add or subtract the areas. Getting pupils in the habit of labeling their sides (a, b and h) helps when introducing trigonometry later. I use the same line “notation” I use when solving equations to reinforce links between substitution into a formula and solving strategies.
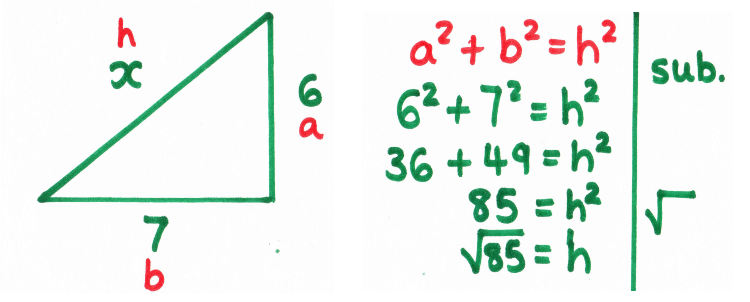
Last year I used a fantastic idea I found on Math Foldables to get pupils to create a little visual reminder that Pythagoras’ theorem is linked to the area of the squares on the sides.

Then it’s time for lots of examples and independent practice! No escaping this – pupils need to spend the time working through problems themselves. One thing I do differently now to when I started teaching is mix up hypotenuse and short side problems; teaching them separately just encourages pupils to learn one method for one and one for the other, whereas they really need to be able to identify if they’re trying to find a hypotenuse or a short side.
3. Don’t shy away from surds
I think this is particularly important for groups of pupils who may go on to A Level, as I still have pupils who don’t understand that the decimal answer a calculator gives is an approximation, not the “exact value”. If your scheme of work allows, teach surds first. Then there’s lots of scope for practising surd simplification at the same time. If not, don’t get the calculators out until they’ve shown they are happy to leave their answers as surds.
4. REAL real life applications
Pythagoras’ theorem is actually really useful for creating right angles in construction or building. Builder’s squares work on the inverse of Pythagoras’ theorem (that if a² + b² = h² then the triangle must contain a right angle). I’ve also used string knotted at intervals to create a 3, 4, 5 triangle to show that, when pulled out straight, it creates a right angle.
5. If all else fails…
We all know that teaching for understanding goes out the window before exams, so if you’ve got pupils who still don’t get Pythagoras’ theorem, SASH (Square Add Square Root to find the Hypotenuse) and SSSS (Square Subtract Square Root to find a Short Side) have worked for me as a very last minute fix.